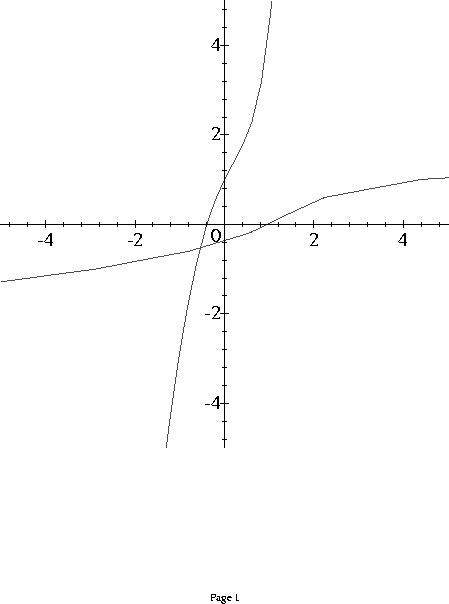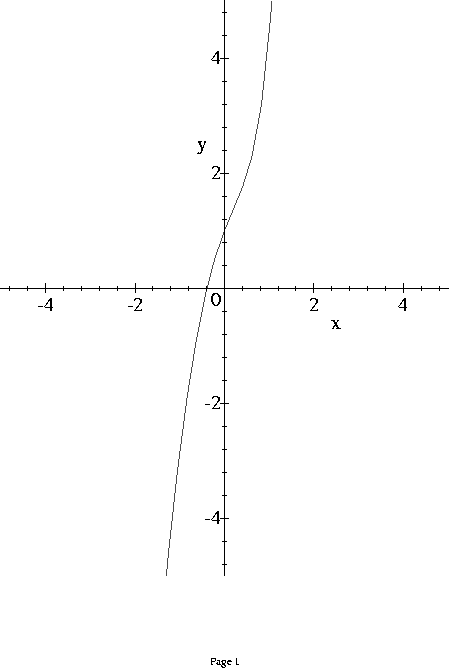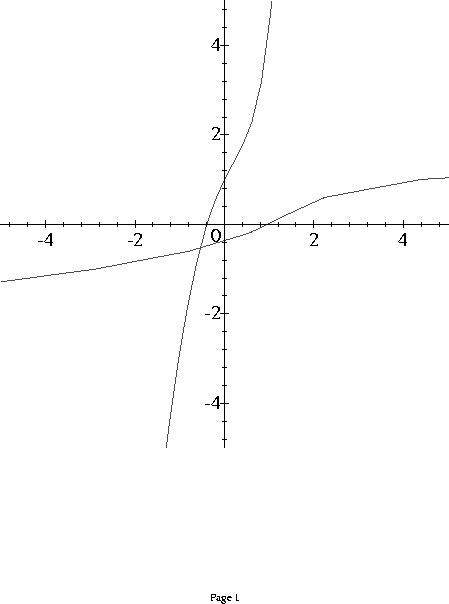MATH 152, Spring 1996 - Exam I
Solutions to Exam 3
PART I - MULTIPLE CHOICE, NO PART CREDIT, NO CALCULATORS
1. Compute the integral Int(x*exp(-x^2),x=0..1)
a) 1/e b) 1/2 c) (1/2)(1-1/e) d) (1/e-1) e) -1/(2e)
SOLUTION: The answer is C. The antiderivative is
2
- 1/2 exp(-x )
Inserting the limits 0 and 1, we obtain -(1-1/e)/2. which is response C.
2. There is a chemical reaction involving the compound N_2 O_5.
Let C(t) denote the concentration of N_2 O_5 as a
function of time t measured in seconds. This
concentration satisfies
dC/dt = -0.05C(t)
How long (in seconds) will the reaction take to reduce the
concentration to 10% of its original value?
a) 10/(e^(-.05)) b) (e^(.05))/10 c) .05/ln(10) d) .05 ln(1/10) e) ln(10)/(.05)
SOLUTION: The answer is E. The solution to the given differential equation
is C(t)=K e^(-.05t), where K is the inititial concentration. We seek the time t
when C(t)=K/10 (one tenth the initital concentration). Setting K/10=K e^(-.05t)
and solving for t (by taking natural logs) gives t=ln(1/10)/(-.05).
Since ln(1/10)= -ln(10), this becomes t=ln(10)/(.05), which is response E.
3. Compute the integral
e
/
|
| x ln(x) dx
|
/
1
a) 1/2 b) (e^2 +1)/4 c) e d) e^2 e) (3e^2)/4 - 1/4
SOLUTION: The answer is b). This is an integration by parts with
u=ln(x) and dv= x dx. This gives an antiderivative of
x^2 ln(x)/2 - x^2/4. Inserting the limits 1..e gives e^2/2 -e^2/4 +1/4
which simplifies to response b).
(keep in mind that ln(e)=1 and ln(1)=0).
4. Compute the integral
/
| 3
| cos(x) dx
|
/
a) -(cos^4 x)/(4sin(x)) +C b) (1/4)cos^4 x +C c) cos(x) -(1/3) sin^3 x +C
d) cos(x) -(1/3) cos^3 x +C e) sin(x) -(1/3) sin^3 x +C
SOLUTION: The answer is e). Write cos^3 as (cos^2) (cos) and then
convert cos^2 to 1-sin^2. The integrand then becomes
cos - (sin^2)cos. The cos term integrates to sin. The (sin^2) cos integrates
to (sin^3)/3 (simple u-substitution). Putting the two pieces together gives e).
5. Which of the following is the graph of y = cosh(x) - sinh(x)?
The repsonses are 5 graphs.
SOLUTION: Note cosh(x)-sinh(x)=(e^x +e^(-x))/2 - (e^x-e^(-x))/2
which simplifies to e^(-x). So the answer is the graph of y=e^(-x).
Find the value of tan(cos^(-1) (3/5)).
a) 5/3 b) 3/4 c) 3/5 d) 4/3 e) 4/5
SOLUTION: The answer is d). We are seeking the tangent of
the angle theta (between 0 and Pi) whose cosine is 3/5.
Note that if cos(theta) = 3/5, then sin(theta) = 4/5
(use the identity cos^2+sin^2=1 and note that sin(theta)
has to be positive since 0 < theta < Pi). Therefore
tan(theta) = sin(theta)/cos(theta) = (4/5)/(3/5) = 4/3 which is response d).
7. Find the equation of the line tangent to the curve y = arcsin(x)
at the point (1/sqrt(2), Pi/4).
a) y= sqrt(2)x/2 +Pi/4-1 b) y= Pi x/4+(Pi/4)(1 -sqrt(2)/2) c) y=sqrt(2)x +Pi/4 -1
d) y= -sqrt(2) x +Pi/4 +1 e) y= - sqrt(2)/2 x +Pi/4 +1
SOLUTION: The answer is c). The derivative of arcsin(x)
is 1/sqrt(1-x^2). Inserting x=1/sqrt(2) gives a slope of 1/sqrt(1/2)
which equals sqrt(2). Therefore the tangent line is y = sqrt(2) x + b,
where b must be Pi/4 -1 inorder for this line to pass through the point (1/sqrt(2), Pi/4).
8. Compute the integral
e
/
| 1
| -------------- dx
| 2
/ x (1 + ln(x) )
1
a) Pi/4 b) Pi/2 c) -3/4 d) ln(2) e) 1/e
SOLUTION: The answer is a). This is a u - substitution problem
with u=ln(x) and du = (1/x) dx. The antiderivative becomes
/
| 1
| ------ du
| 2
/ 1 + u
which is arctan(u) = arctan(ln(x)). Inserting the limits 1..e, we
get arctan(ln(e)) - arctan(ln(1)) = arctan(1)-arctan(0) = Pi/4,
which is response a).
9. Evaluate the following limit: lim_(x -> infinity) ln(5+e^x)/ 5x.
x
ln(5 + e )
lim 1/5 ----------
x -> infinity x
a) 0 b) infinity c) 1 d) 1/5 e) ln(5)
SOLUTION: The answer is d). When x is large ln(5+e^x) is nearly
the same as ln(e^x) which simplifes to x. Therefore the given limit is
the same as the limit of x/(5x) as x -> infinity, which is 1/5 or response d).
10. Use the trapezoid rule with n=2 to approximate the
integral
2
/
| 3 1/2
| (1 + x ) dx
|
/
0
a) 2+ sqrt(2) b) 2(2+sqrt(2)) c) 4(2+sqrt(2)) d) (1/2)(4+sqrt(2)) e) 4+sqrt(2)
SOLUTION: The answer is a). Let f(x) be the integrand. The step size is 1
and so trapezoidal rule is (f(0)/2 +f(1) +f(2)/2) (1), which evaluates to
1/2 + sqrt(2)/2 + 3/2 = 2 + sqrt(2)
WORK OUT PROBLEMS with PARTIAL CREDIT
CALCULATORS ARE PERMITTED. SHOW ALL WORK
11. Find y' if
(3 x)
y = (1 + 2 x)
SOLUTION: This is a logarithmic differentiation problem.
ln(y)= (3x) ln(1+2x). Differentiate and obtain
y'/y = 3 ln(1+2x) + (3x)(2)/(1+2x)
So y' = y(3 ln(1+2x) + 6x/(1+2x))
= (1+2x)^(3x) ( 3 ln(1+2x) +6x/(1+2x))
12. An object with an initial temperature of 150 degrees is
allowed to cool in a room whose temperature is 25 degrees
If, after 10 minutes, the temperature of the object has
dropped to 120 degrees what is the temperature of the
object after 30 minutes? Assume Newton's Law of Cooling
which states that the rate of cooling of an object is proportional to the
temperature difference between the object and its surroundings.
SOLUTION: The differential equation for Newton's law of cooling is
dy/dt = k (y- 25) (rate = k * (difference in temperature))
The solution is obtained by separation of variables;
dy/(y-25) = k dt which integrates to ln(y - 25) = kt+c.
This exponentiates to y-25 = Ce^(kt) or
y= 25 + C e^(kt)
Since y=150 when t=0, we get C = 125. Since y = 120 when t = 10,
we get 120 = 25 + 125 e^(10k) or k = (1/10) ln(95/125).
We wish to find the temperature at t=30, which is
25+125*exp(30k) = 79.87 degrees.
13. Do one of the following:
a) Compute
/
| 1
| ------------ dx
| 2
/ x + 2 x - 3
SOLUTION:
The denominator factors as (x-1)(x+3).
Write the integrand as A/(x-1) + B/(x+3) - - partial fractions.
The numerator of this is A(x+3) + B(x-1) = (A+B)x + (3A-B).
This has to match with the numerator of the integrand, which is 1.
Therefore, we get the equations 1= 3A-B and A+B = 0 with solutions
A=1/4 and B= -1/4. So the integral becomes
/
| 1 1
| ------- - -------- dx
| 4 x - 4 4 x + 12
/
which integrates to ln(4x-4)/4 - ln(4x+12)/4 + C.
b) Let E_S be the error in approximating
b
/
|
| f(x) dx
|
/
a
by Simpson's rule. It is known that E_S is bounded by
|E_S| <= K(b-a)^5 / ( 180 n^4},
where n is the number of subintervals (n must be even)
and K is the maximum of |fourth derivative of f| on the interval a <= x <= b.
Using the bound on E_S given above, what is the minimum even number, n, needed to approximate
2
/
| 3 1/2
| (1 + x ) dx
|
/
0
with an accuracy of 10^{-8). You may use the fact that
the maximum value of the fourth derivative of sqrt(1+x^3)
on the interval 0 <= x <= 2 is 8.
SOLUTION: Using K=8 and b-a = 2, in the above estimate, we get
8*32 *10^8
------------ <= n^4
180
Taking 4th roots we get that n must be larger than the fourth root
of (8*32)/180 multiplied by 10^2, which simplifies to 109.2. Since
n must be an even integer, the answer is 110.
1.092048345
14. Let R be the region inside the circle x^2 + y^2 = 1 and to
the right of the line x = 1/2. Find the area of R.
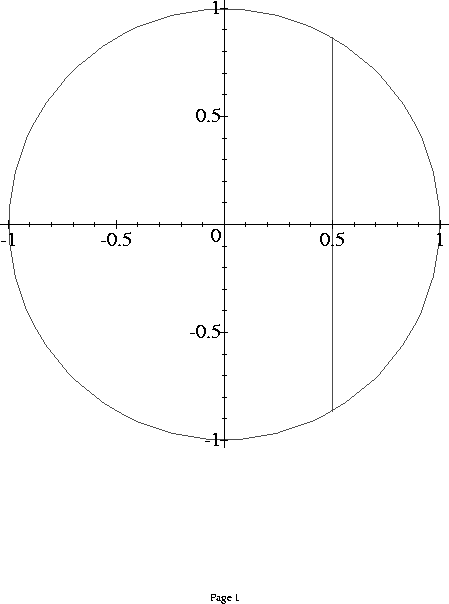
SOLUTION
Solving for y gives y=sqrt(1-x^2)
The integral that represents the area is
1
/
| 2 1/2
2 | (1 - x ) dx
|
/
1/2
To integrate this expression, use a trig substitution x=sin(t) dx = cos(t) dt
We have 2 sqrt(1-x^2) dx = 2 sqrt(1-sin^2 ) cos = 2 cos^2 (t).
From a standard trig identity, 2 cos^2 (t) = 1+ cos(2t),
which integrates to t+sin(2t)/2 which by the double angle
formula is t + sin(t) cos(t). Since x= sin(t) and cos(t) = sqrt(1-x^2),
the antiderivative is sin^(-1) (x) + x sqrt(1-x^2). Inserting the limits
gives
1/2
1/3 Pi - 1/4 3
as an answer.
15. Below is the graph of f(x) = e^(2x) - 3x^2.
Add the plot of the inverse g(x) = f^(-1) (x) and then
compute g'(1).
SOLUTION: g'(1) = 1/f'(a) where a is the number
with f(a)=1 or e^(2a) - 3a^2 = 1.
By inspection, the solution is a=0.
So we need to compute 1/f'(0).
Now f'(x) = 2 exp(2x) - 6x, and so f'(0) = 2.
Therefore g'(0) = 1/2.