Theoretical Numerical Analysis
Theoretical numerical analysis plays a fundamental role in guiding both the understanding of how efficient numerical algorithms should be designed and how they should behave when implemented. Typical issues involve the stability, convergence and robustness of proposed methods as well as the design and analysis of iterative methods for the solution of the resulting linear and non-linear systems of equations. Recent activities in this area include the following:
Adaptive Methods on Surfaces and the Laplace-Beltrami Operator
|
Because of its relation with curvature of surfaces, the Laplace-Beltrami operator (or surface Laplacian) is inherent to any geometrically driven free surface problem (e.g. capillary flows). Its mathematical understanding is therefore critical in this context. Standard adaptive strategies do not translate directly on surfaces (to capture the geometry). A geometric consistency dictated by the Laplace-Beltrami operator is required. We developed this concept along with its analysis and proposed an algorithm ensuring geometric consistency (see illustrations for the refinement procedure on the right). This naturally raises the question of designing an efficient solver for the Laplace-Beltrami problem. We developed uniformly convergent (with respect to the number of grids) variational and nonvariational multigrid solvers for such operator. Finally, we initiated the description of optimal adaptive methods on surfaces. As a first step, our aim is to determine the best approximation rate of the solution to the Laplace-Beltrami equation. To achieve this, an intriguing trade-off between the regularity of the surface and the right hand side data is required. |

Total curvature of the unit sphere.

Approximation to the unit sphere total curvature after a standard uniform refinement: some curvatures are inverted, the others are over amplified.

Approximation to the unit sphere total curvature after a geometrically consistent mesh refinement.
|
| Back to Top |
Far Field Boundary Conditions for Scattering Problems
|
This research involves the development and analysis of efficient ways for implementing far field boundary conditions for scattering problems on unbounded domains. The fundamental technique under investigation is the so-called "perfectly matched layer(PML)." From an engineering point of view, this technique involves the use of a ficticious highly absorbing layer outside of the region of interest specifically designed to absorb all outgoing radiation. Mathematically, the method is related to a complex change of coordinate system. The PML approximation preserves the solution in the region of interest while exponentially decaying in the PML region. This suggests domain truncation and the approximation by finite elements on the bounded (truncated) domain. Professors Bramble and Pasciak and Dr. Kim (2009 Ph.D) have recently developed a new theoretical understanding of the PML in Cartesian geometry. This was based on locating the essential spectrum of the PML operator. With this information, it is possible to deduce variational stability (and hence convergence of truncated finite element approximations) from uniqueness at points in the complement of the essential spectrum. Local Researchers: J.H. Bramble and J.E. Pasciak. |
A PML approximation.
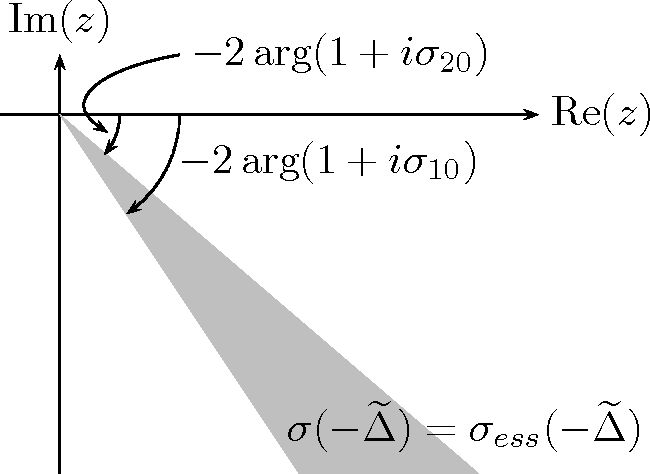
Essential spectrum of a Cartesian PML operator.
|
| Back to Top |
Tuning-Free Adaptive Multilevel Discontinuous Galerkin
Methods for Maxwell's Equations
|
This project focuses on the development, analysis and implementation of adaptive multilevel Discontinuous Galerkin (DG) methods for coupled interior/exterior domain problems associated with the time-harmonic Maxwell equations. Such problems are of great relevance in numerous applications including the scattering of electromagnetic waves by conducting bodies. Numerical approximations can be obtained by finite element methods for the interior domain problem combined with several different options to handle the exterior domain problem. We will consider the use of a Dirichlet-to-Neumann map with high order Fourier expansion, the perfectly matched layer (PML) and also a high-order local radiation boundary condition for solving the exterior problem. The PML has the advantage of being a differential formulation which can be discretized by finite element methods with minimal modification. We choose to use DG discretizations as they have recently proven to be a computationally attractive alternative to curl-conforming discretizations by edge elements of Nédélec's first or second family. The DG methods will be realized by multilevel techniques on the basis of an adaptively generated hierarchy of triangulations of the computational domain. Emphasis of the research activities is on three central issues related to the basic steps `SOLVE', `ESTIMATE', `MARK', and `REFINE' of the adaptive loop. First, the smoothing process within the multilevel solver will be performed only on the newly refined part of the triangulation obtained by a residual type a posteriori error estimator. Second, the a posteriori error analysis, which additionally has to take into account the effect of such local smoothing, aims to provide conditions guaranteeing a reduction of the global discretization error at each refinement step. Third, the selection of elements, faces and edges of the triangulation for refinement will be based on a bulk criterion with an automatic ('tuning free') choice of the parameters controlling the amount of refinement in order to achieve optimal performance of the overall algorithm. Finally, we will propose criteria to choose the parameters of the DtN and the PML automatically, such that no tuning on behalf of the user is required there as well. Local Researchers: G. Kanschat and S. Tan. |
|
| Back to Top |
L1 Minimization Techniques for PDEs, Surface Reconstruction,
and Image Enhancement
|
The objective of this project is to develop L1-based minimization techniques to solve problems with limited smoothness. The problems under consideration could be partial differential equations with discontinuous solutions (nonlinear conservation laws) or discontinuous gradient (steady Hamilton-Jacobi equations). This question arise also in geometric modeling and image reconstruction when one tries to reconstruct a piece-wise smooth surface or image from a coarse set of measurements. The objectives could vary with the applications but the intuitive goal is to preserve the shape of the object. For example, one may want to reconstruct a convex body if the underlying data comes from a convex object, a flat surface if the data is locally flat, or preserve a particular structure of the level sets. The main superiority of the L1 setting over the more traditional L2-based methods is that it is non-oscillatory and sparse. The idea of using the L1-metric instead of the more traditional L2-metric is exploited in many different areas with great success (compressed sensing, image de-noising, surface reconstruction). Professors J.-L. Guermond and B. Popov have been developing a research program in this field since 2004. They have proved that the L1 setting is optimal to compute viscosity solutions of steady Hamilton Jacobi equations. They have proposed a reconstruction for images and surfaces based on minimizing a K-functional comprising the L1-distance between the reconstructed field and the noisy data plus the total variation of the gradient of the reconstructed field. Local Researchers: J.-L. Guermond and B. Popov. |
Cubic image enhancement.
 
Cubic image enhancement.
 
Cubic non-oscillatory surface reconstruction.
 
Cubic non-oscillatory terrain reconstruction.
|
| Back to Top |
Lumped Mass FEM for Parabolic Problems
|
The objective of this project is study the error of lumped mass finite element approximations of parabolic problems with non-smooth initial data while using piece-wise linear polynimoals. The lumped mass method has the advantage over the standard Galerkin method that, under the assumption that the triangulation is of Delaunay type, the solution satisfies the maximum-principle (see, e.g. the monograph, V. Thomee, Galerkin Finite Element Methods for Parabolic Problems, Springer-Verlag, Second Edition, Berlin, 2006). The main outcome of this research is that the known optimal error estimates for standard semidiscrete Galerkin finite element method carry over to the luped mass methods as long as the initial data is in the Sobolev space H1. For inital data in L2 only there is a loss in the convergence rate, except in the case when the finite element mesh has symmetry property at each mesh point. This research has been reported in the paper P. Chatzipantelidis, R. Lazarov, and V. Thomee, Some error estimates for the lumped mass finite element method for a parabolic problem (to appear in Mathematics of Computation) and available as an ISC Technical Report. Local Researchers: R.D. Lazarov |
Mesh with symmetry at a point
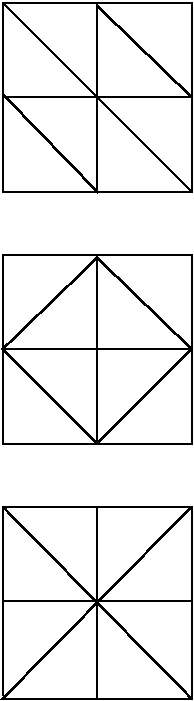 |
| Back to Top |
Hybridization of DG FEM for Elliptic Problems
|
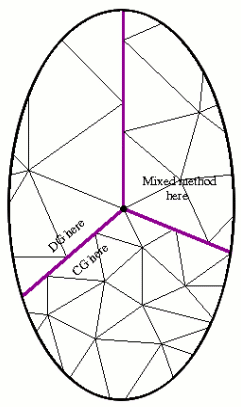
Hybridizable DG (HDG) methods were first introduced in our paper: B. Cockburn, J. Gopalakrishnan, and R. Lazarov Unified Hybridization of Discontinuous Galerkin, Mixed, and Continuous Galerkin Methods for Second Order Elliptic Problems, SIAM J. Numer. Anal., v.47 (2), 1319-1365 (2009) available here. HDG methods are DG methods very close to mixed finite element methods. They share the advantages of mixed and DG methods. E.g., while maintaining the size and sparsity identical to mixed methods, HDG methods offer greater choices in approximation spaces, because of its flexible stabilization mechanism. What can hybridization achieve that is difficult to obtain by conventional techniques ? The list could be made quite long. This includes:
Local Researchers: R.D. Lazarov |
Coupling methods (an application discussed in our paper)
|
| Back to Top |
