A numerical subgrid method for Brinkman equations in highly heterogeneous media
|
Table of contents: |
|
|
|
Mathematical background. Historically, flows of incompressible fluid in porous media in a domain $\Omega$ have been modeled by Darcy relation between the macroscopic pressure $p$ and velocity $u$: $ ~~\nabla p = - \mu \kappa^{-1} u$, with $\kappa$ being the permeability tensor and $\mu$ the viscosity. However, for highly porous materials such as glass or mineral wool with porosity above 0.98 or open foams with porosity above 0.95, Darcy's based prediction deviate substantially from the measurements. To reduce the discrepancy, Brinkman in 1947, enhanced the Darcy's law by adding dissipative term scaled by the viscosity. This led to the following system
$$ -\mu \Delta u + \nabla p + \mu \kappa^{-1} u = f, \quad \nabla \cdot u = 0, \quad \texttt{in~} \Omega.$$
where, $\Omega \subset \mathbb{R}^d$ with $d=2,3$ is the domain of the highly porous media, $f$ is a given internal dragging force (for instance gravity), and the unknowns are the velocity $u$ and the pressure $p$. This system must be complemented with suitable boundary conditions.
Finite element approximation. In many applications, one needs to know about the interior composition of a body without invasive procedures. To resolve the fine scale features we shall use a subgrid approach, a finite element method based on two scales of quasi-uniform quadrilateral triangulations of $\Omega$, $ {T}_H$ and ${T}_h$ with mesh-size parameter $H$ and $h$, respectively. Each $T \in {T}_H$ is an agglomeration of elements in $T_h $. With the partitions ${T}_H$ and ${T}_h$ we associate finite element spaces $({V}_{H}, {W}_{H})$ and $({V}_{h}, {W}_{h})$, respectively. The spaces $V_h$ and $V_h$ are based on BDM1 finite elements, that are $H(div)$-conforming while $W_H$ and $W_h$ consist of piece-wise constant functions. This will lead to a discontinuous Galerkin method which was studied by Wang and Ye in 2007 (SINUM, v.45). The coarse grid finite element spaces $({V}_{H}, {W}_{H})$ and its fine grid enhancement $(\delta V_h,\delta W_h)\subset({V}_{h},{W}_{h})$ that consists of coarse mesh bubbles defined on the fine grid are chosen in such a way that:
$$ (i) \quad \nabla \cdot \delta V_h = \delta W_h \quad and \quad \nabla \cdot V_H = W_H, $$
$$ (ii) \quad \delta W_h \perp W_H \quad in \, \, the \, \,L_2-inner \, product, $$
$$ (iii) \quad V_H \cap \delta V_h=\{{0}\}. $$
The finite element approximation is obtains from a discontinuous Galerkin method for the Brinkman system on the space $(V_H \oplus \delta V_h, W_h \oplus \delta W_h)$. The numerical subgrid approach for problem stated above is essentially analogous to the work of Arbogast of 2004 (SINUM, v. 42). Namely, the weak form of the above equations posed with respect to the two-scale space $(V_H \oplus \delta V_h, W_h \oplus \delta W_h)$, i.e.: Find $(u_{Hh}, p_{Hh})\in (V_H \oplus \delta V_h, W_h \oplus \delta W_h)$ such that for all $(v_{Hh}, q_{Hh} )\in (V_H \oplus \delta V_h, W_h \oplus \delta W_h)$ we have
$$ a(u_{Hh}, v_{Hh})+ b(v_{Hh}, p_{Hh}) + b(u_{Hh}, q_{Hh}) = F(v_{Hh}).$$
The bilinear form $a(\cdot, \cdot)$ corresponds to the DG Galerkin approximation of $ -\mu \Delta u + \mu \kappa^{-1} u $ part of Brinkman's equation and $b(v, p)=(\nabla \cdot v, p)$. Since there is unique representation of any function in $(u_{Hh}, p_{Hh})\in (V_H \oplus \delta V_h, W_h \oplus \delta W_h)$ as $u_{Hh}= u_H + \delta u_h$ and $p_{Hh}=p_h + \delta p_h$ with $(u_{H}, p_{H})\in ( V_H, W_H)$ and $(\delta u_{h}, \delta p_{h})\in (\delta V_h, \delta W_h)$ we can test separately with $(v_H,q_H)$ and $(\delta v_h, \delta q_h)$. Due to the properties (i) -- (iii) on the fine-grid we get the problem: find $\delta u_h \in \delta V_h$ and $\delta p_h \in \delta W_h$, such that
$$ a(\delta u_h + u_H, v_h)+ b(v_{h}, \delta p_{h}) + b(\delta u_{h}, q_{h})= F(v_{h})$$
for all $ v_h \in \delta V_h$ and $ q_h \in \delta W_h$. If here we consider $u_H$ as data, we can recover the fine-grid response to the coarse-grid data $(\delta u_h(u_H), \delta p_h(u_H))$, a solution of the above equation with $F=0$. Similarly, one can get the fine-grid response $(\delta u_H(F), \delta p_H(F)) $ to the data $F$. These two problems are solved one each coarse element independently. Replacing these in the coarse-grid equation we get the following identity for all $v_H \in V_H$ and $q_H \in W_H$:
$$ a(u_H + \delta u_h(u_H), v_h + \delta v_h(v_H))+ b(v_{H}, p_H) + b(u_{H}, q_{H})= F(v_{H}).$$
We call this subgrid finite element method. The final solution is $(u_H + \delta u_h(u_H) + \delta u_h(F), p_H + \delta p_h(u_H) + \delta p_h(F)) $. Through the fine-grid corrections $\delta u_h(u_H) + \delta u_h(F)$ and $\delta p_h(u_H) + \delta p_h(F)$ this solution incorporates fine-grid features. Note, that this method involves solving local problems on the fine grid and a global problem on the coarse grid.
DD Schwarz method. The sub-grid approximation exhibits resonance errors along the coarse mesh interfaces. To eliminate this error we can solve the fine grid approximation using as a preconditioner the subgrid method in an overlapping Schwarz domain decomposition manner. Our numerical experiments show that we can eliminate most of the interface error after few iterations. This is shown on the figures below.
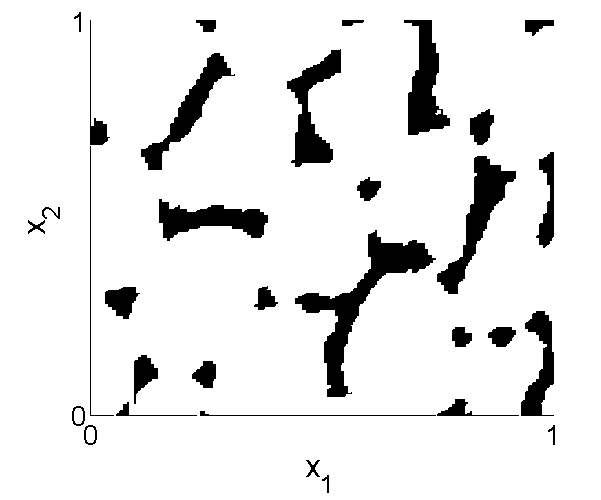
Numerical Examples. Here we shall consider four sample geometries: open foam, vuggy media, and SPE10.
|
|
|
|
|
|
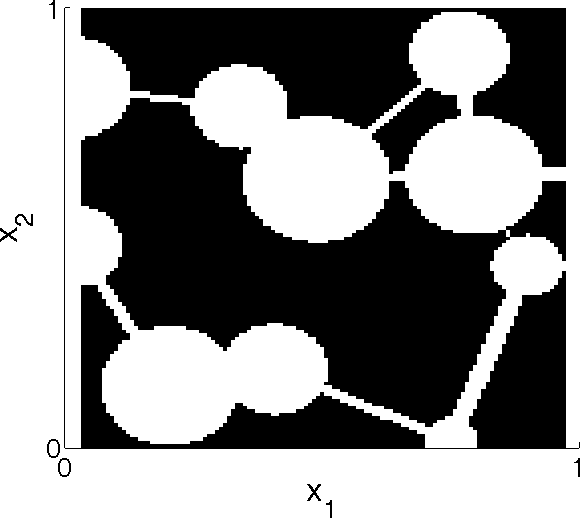
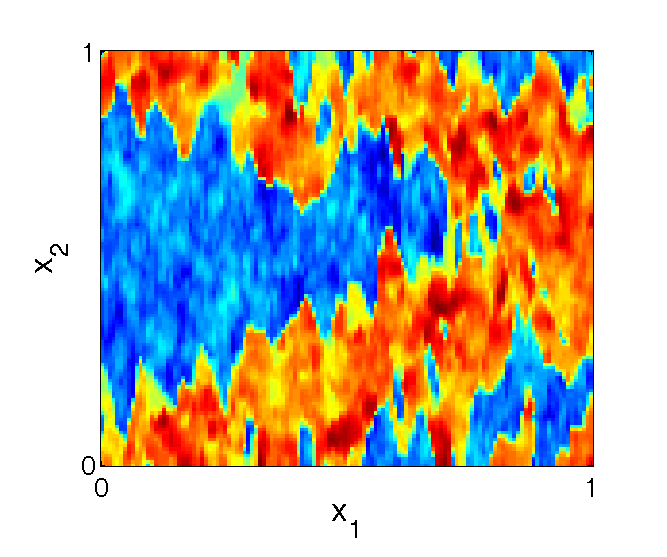
Periodic structure |
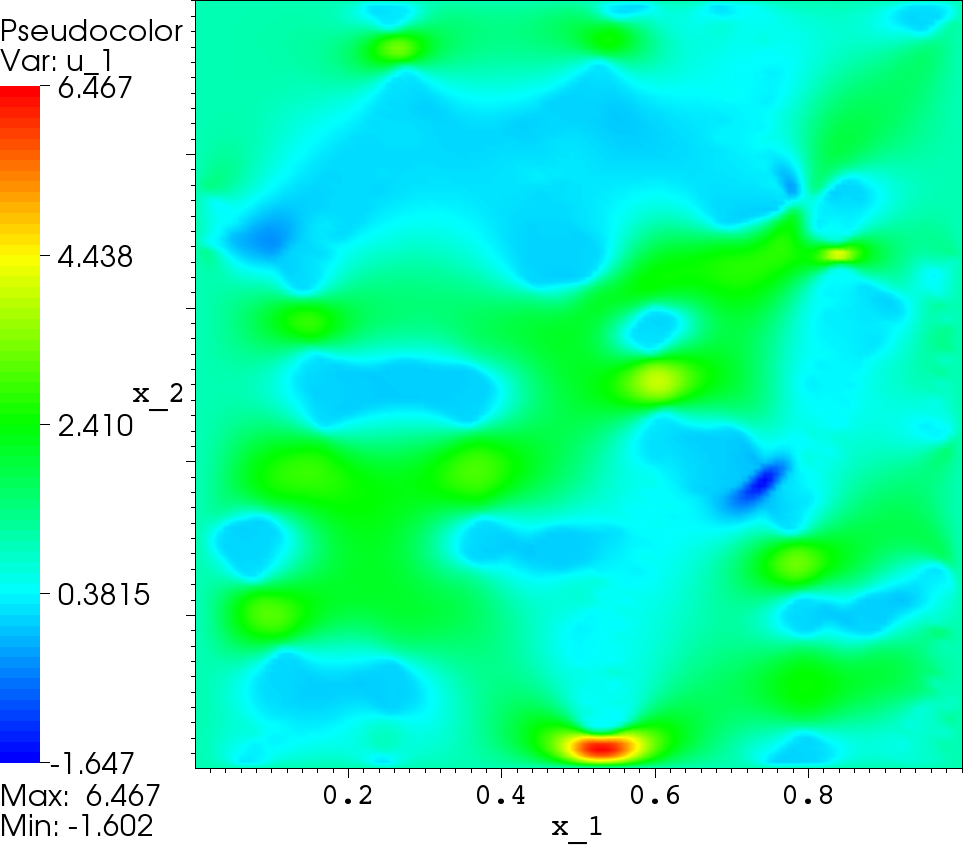
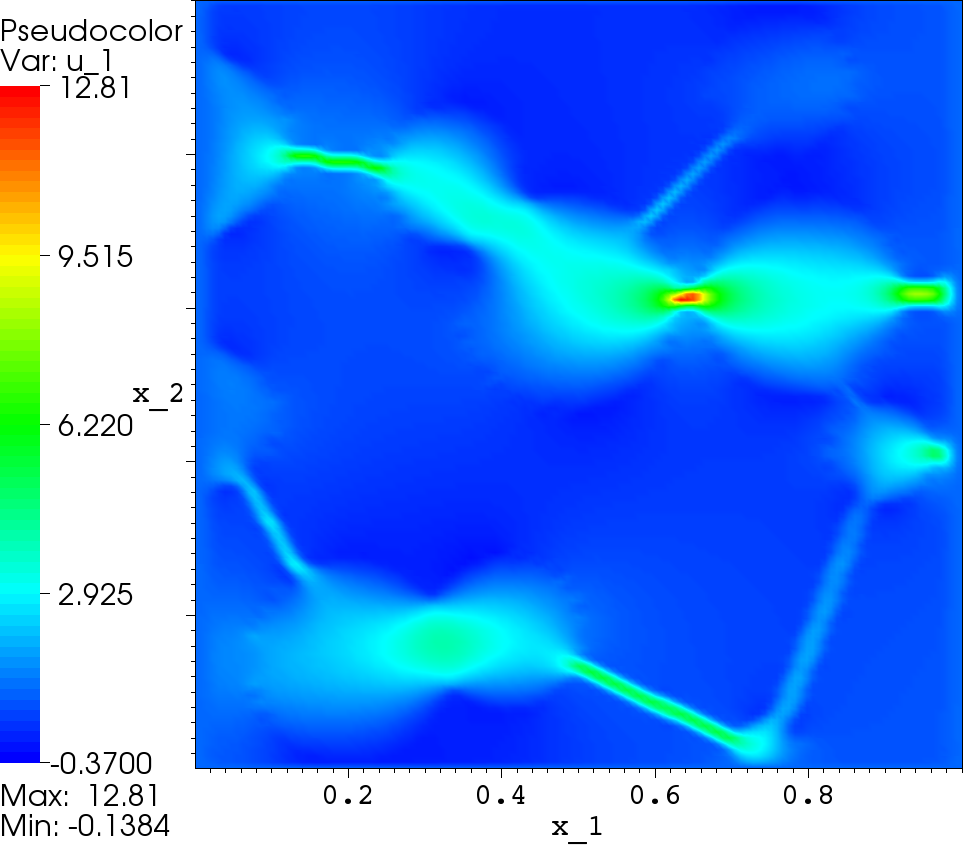
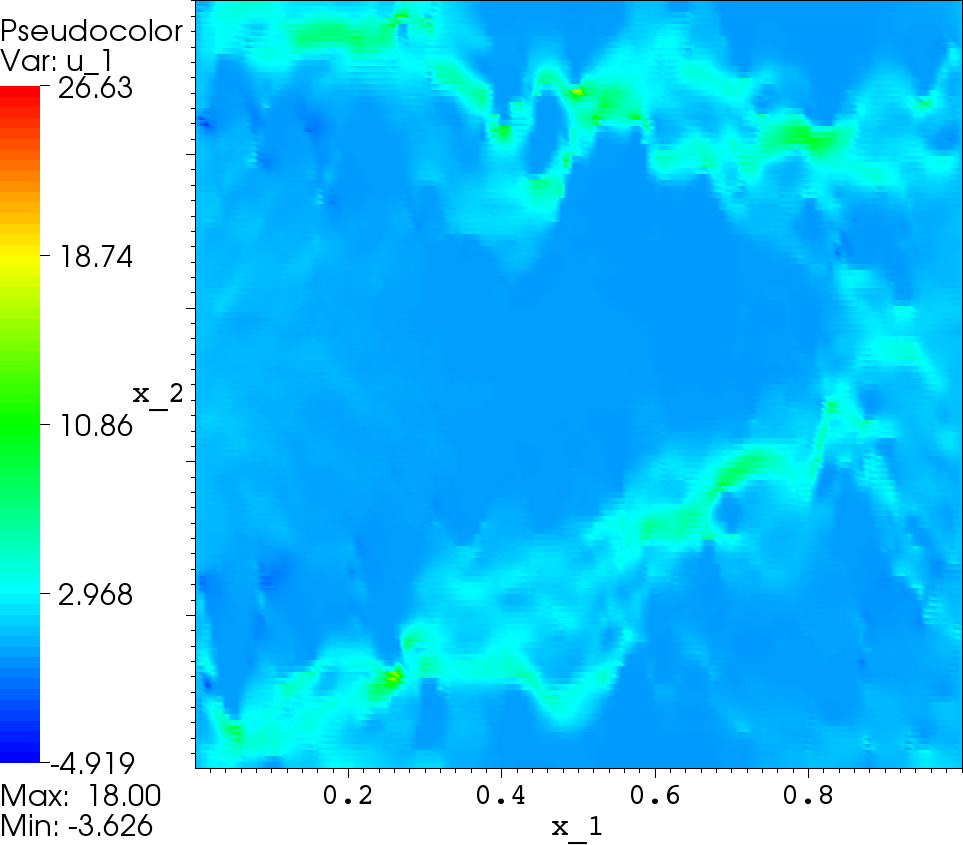
Reference solution |
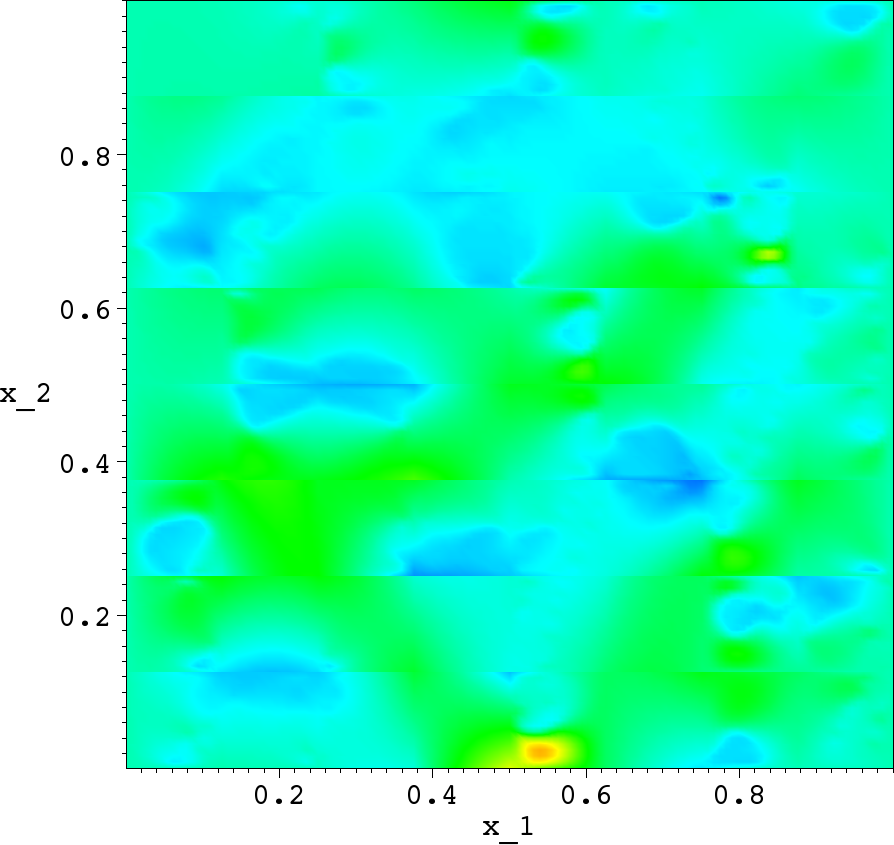
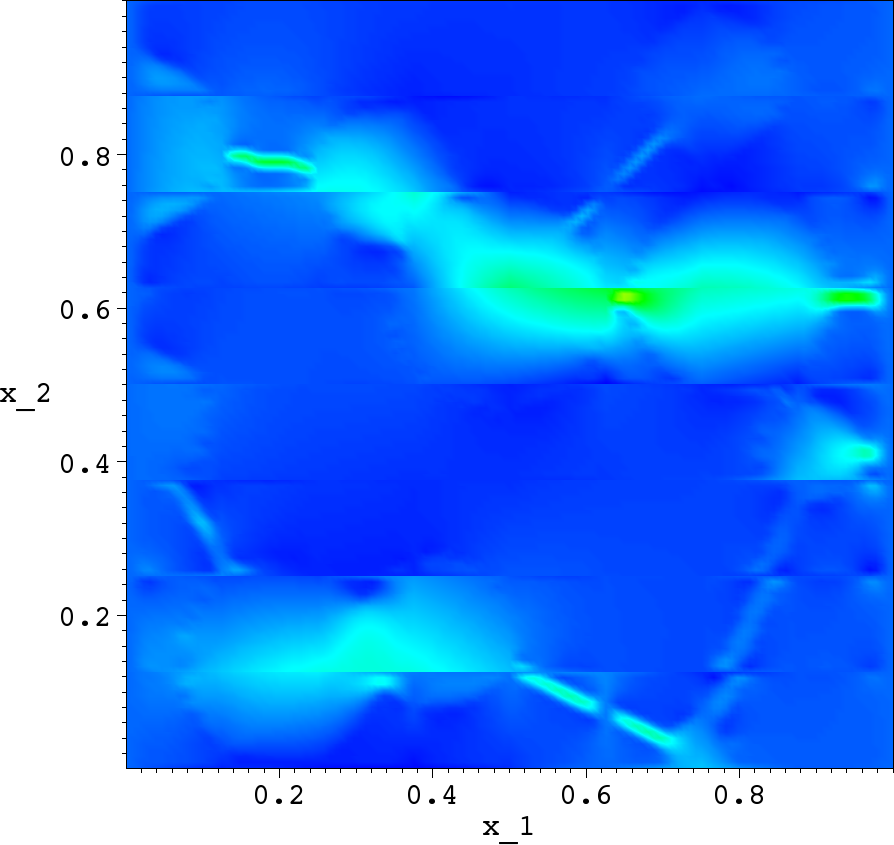
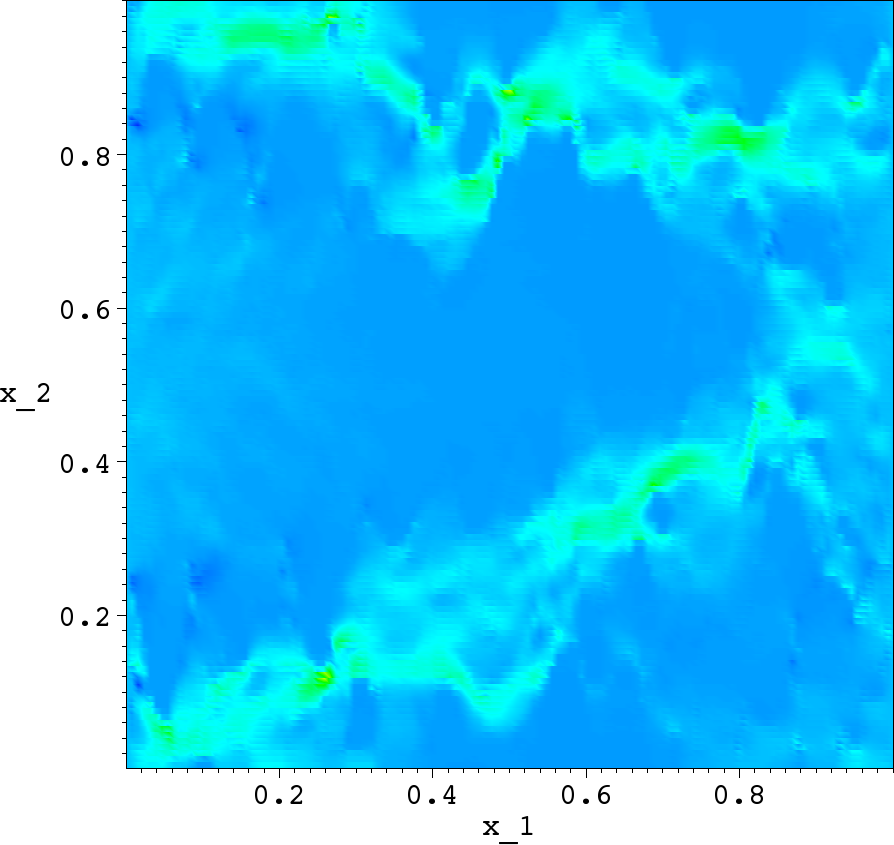
Subgid solution |
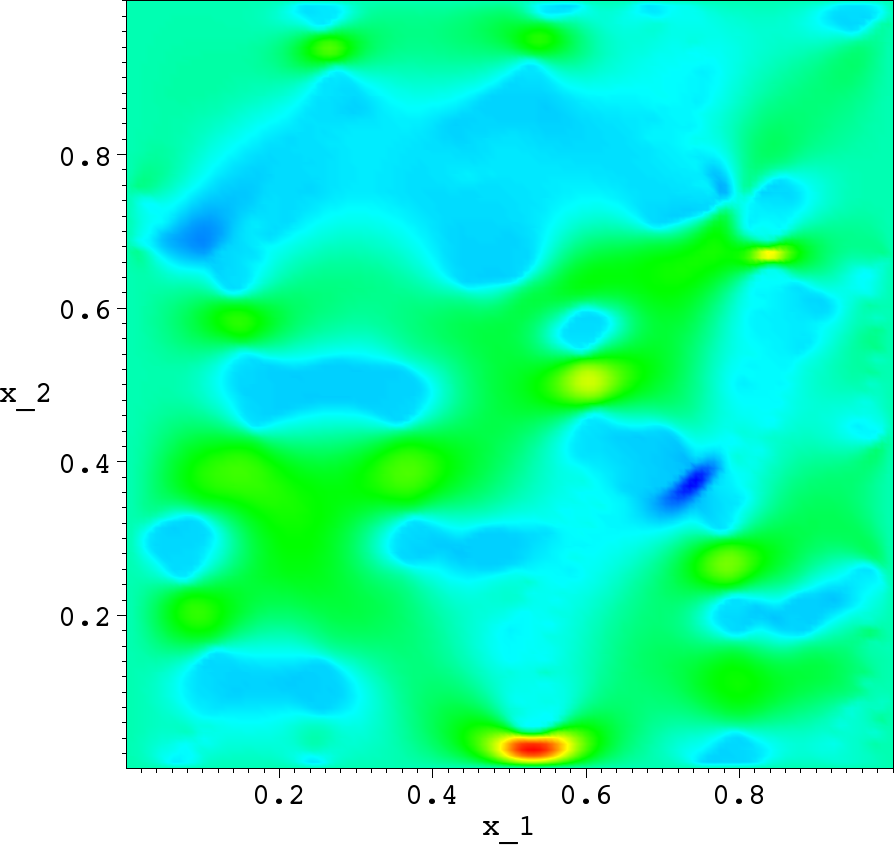
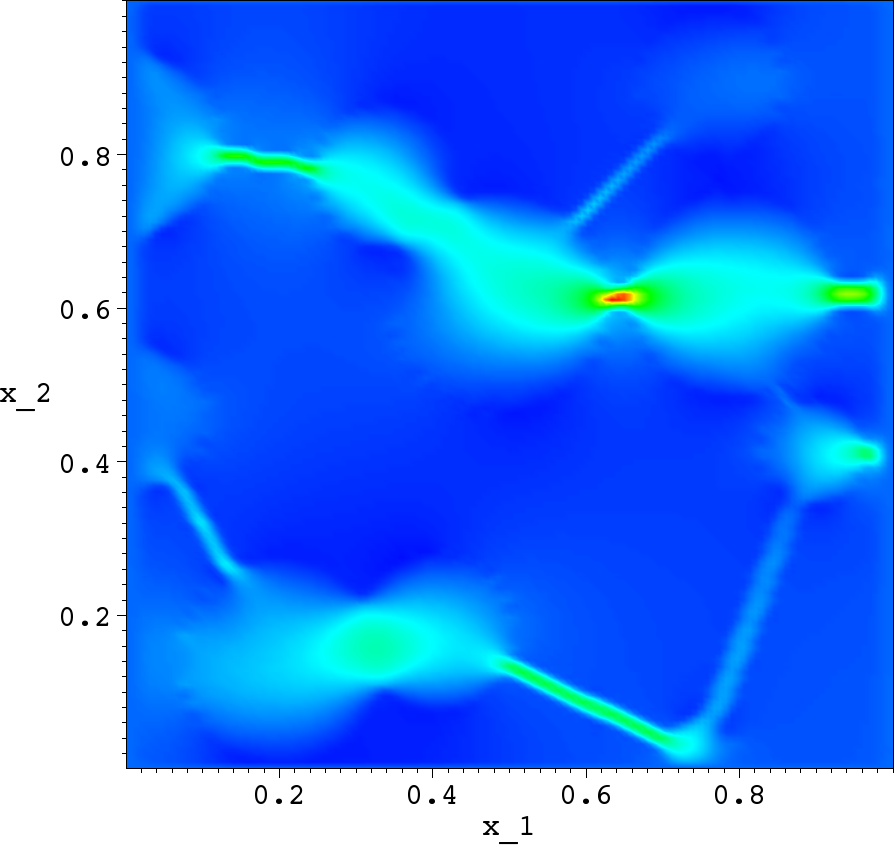
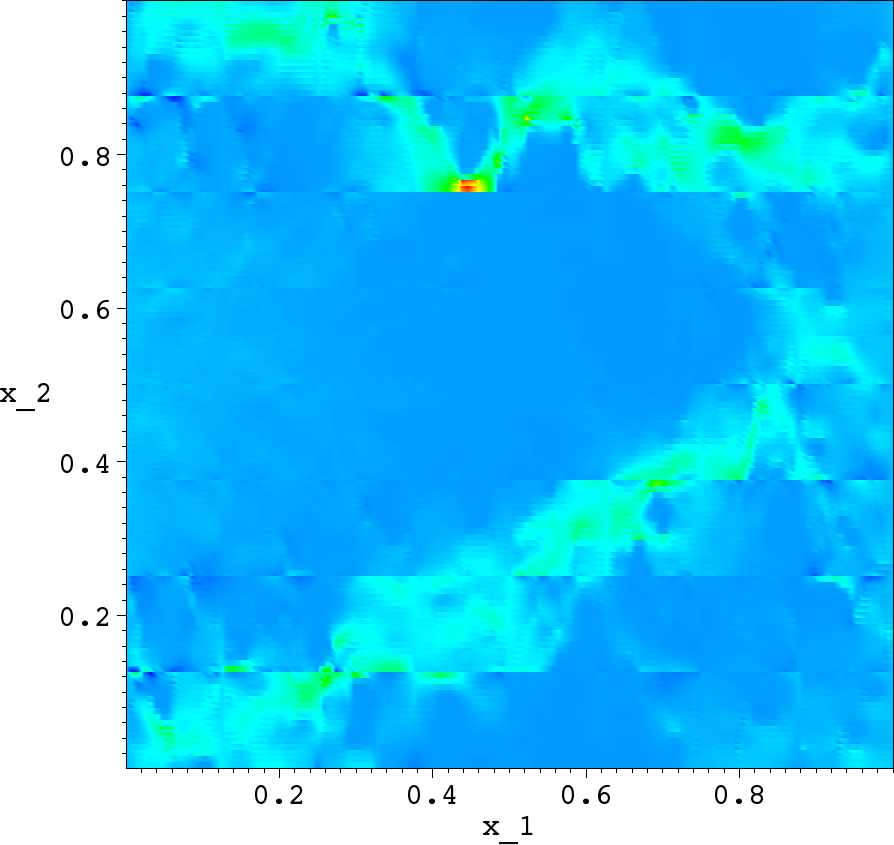
Solution after 5 Schwarz iter. |
|
|
|
|
|
|
Vuggy media |
Reference solution |
Subgid solution |
Solution after 5 Schwarz iter. |
|
|
|
|
|
|
SPE10 slice |
Reference solution |
Subgid solution |
Solution after 5 Schwarz iter. |
From the numerical experiments one can make the following conclusions:
- the subgrid FEM provides quite good solution with substantial details due to the heterogeneous character of the media on a faily coearse meshes;
- there are obvious errors along the coarse mesh intefaces (called resonanse errors);
- Schwarz overlapping iterative method improves the accuracy very rapidly, in almost all computations the error is reduced to less than 1% in five Schwarz iterations.
Last revision, April 27, 2010