Least Squares Problems

  1. Least-squares data fitting. The table below contains data obtained by measuring the concentraion of a drug in a person's blood. Find and sketch the straight line that best fits the data in the discrete least squares sense.

    Log of Concentration
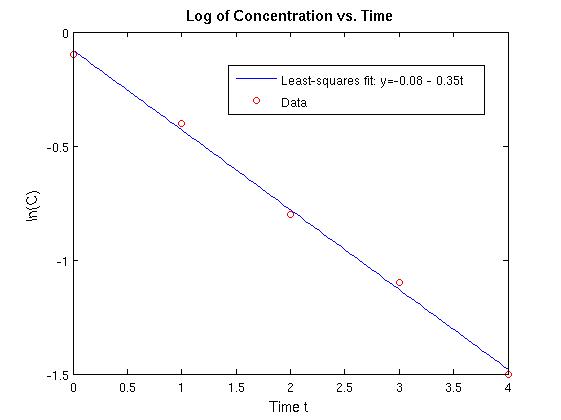
    t  0  1  2  3  4
    ln(C)   − 0.1  − 0.4  − 0.8  − 1.1  − 1.5

    Solution. We want to find coefficients c1 and c2 such that y = c + c2t is the best straight line fit to the data. L1et u1 = [1 1 1 1 1]T, u2 = [0 1 2 3 4]T, and yd = [-0.1 -0.4 -0.8 -1.1 -1.5]T. Let S = span{u1, u2}. Doing a straight-line fit amounts to solving the least squares problem of finding p such that
    || yd − p || = minu ∈ S || yd − u ||,
    where the norm and inner product are the standard ones for R5.

    The Gram matrix G in this case has entries G11 = u1Tu1 = 5, G12 = u2Tu1 = 10, G21 =G12 = 10, and G22 = u2Tu2 = 30. Thus, G =
     5  10
     10  30

    In this problem the vector vector d = (u1Tyd   u2Tyd)T = (− 3.9   − 11.3)T. Solving Gc = d, we get c = (−0.08 −0.35)T. Thus is the intercept and slope are c1 = −0.08 and c2 = −0.35. The line we want is y = - 0.08 - 0.35t.

  2. Least squares fitting of a function. We want to find the quadratic polynomial that gives the best least least squares fit for the function f(x) = e2x on the interval [-1,1]. In this case, the inner product and norm are
    < f , g > = ∫ −11 f(x)g(x)dx and ||f|| = (∫ −11 f(x)2dx)½.
    The subspace S = P3 = span{1,x,x2}. Instead of using the basis {1,x,x2}, we will use the basis

    p0(x) = 2-1/2,   p1(x) = (3/2)1/2x,   and   p2(x)= (5/8)1/2(3x2-1).

    These polynomials are called normalized Legendre polynomials and they are orthonormal: <pi, pj> = δij. In this basis, the quadratic polynomial that is the best least squares fit to e2x has the form

    p(x) = c1p0(x) + c2p(x) + c3p2(x).

    Recall that when we use an orthonormal basis, the Gram matrix turns out to be the identity: G = I. The equation Gc = d thus becomes c = d. Doing the appropriate inner products we see that

    c1 = d1 = < f, p0> = ∫ −11 e2xp0(x)dx = 8-1/2(e2 - e-2)
    c2 = d2 = < f, p1> = ∫ −11 e2xp1(x)dx = (3/32)1/2(e2 + 3e-2)
    c3 = d3 < f, p2> = ∫ −11 e2xp2(x)dx = (5/128)1/2(e2 - 13e-2)

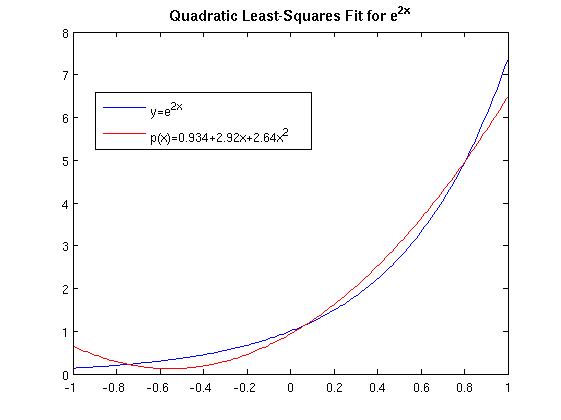
    The quadratic polynomial that is the best least squares fit to e2x is
    p(x) = (1/4)(e2 - e-2) + (3/8)(e2 + 3e-2)x + (5/32)(e2 - 13e-2)(3x2-1).

    Both the function and quadratic least squares fit are plotted below.