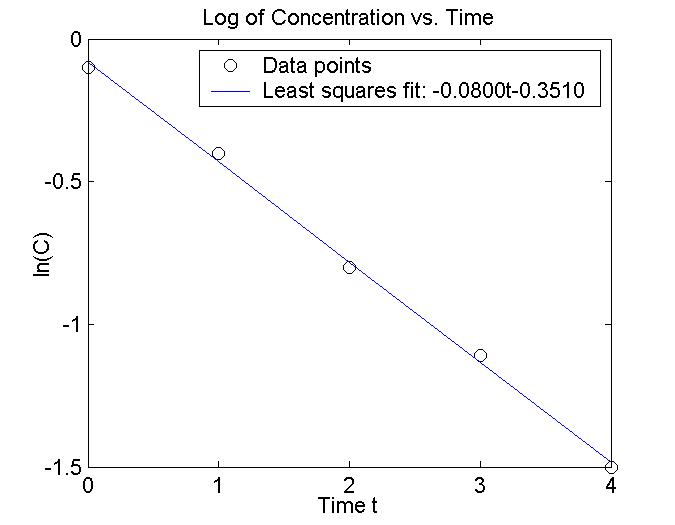
| t | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| ln(C) | -0.1 | -0.4 | -0.8 | -1.1 | -1.5 |
Solution Let U = [1 1 1 1 1]T, V = [0 1 2 3 4]T, and Y = [-0.1 -0.4 -0.8 -1.1 -1.5]T. To do a least squares fit of a straight line to the data, we need to find a and b such that ||Y - aU -bV|| is a minimum. The norm and inner product are the standard ones for R5 divided by 5. (We could skip division by 5. It will not change to the answer.) This is equivalent to finding W in the span of U and V that minimizes ||Y - W||. Recall that we showed that there is a unique solution to this problem,
W = p = < Y, U1> U1 + < Y, U2> U2,
where U1, U2 form an orthonormal basis for the span of U and V. To obatin a and b, we could use Gram-Schmisdt to find an orthonormal set - U1 = U and U2 = (V - < Y, U1> U1)/||V - < Y, U1> U1|| works. Find p from the formula above and then switch back to the original basis.There is a more direct way to solve this problem, however.Again from class, we recall that the minimizer p is the only vector with the property that < Y -p, W> = 0 for all W in the span of U and V. We know that p = aU + bV, by what we said
< Y -p, U> = 0 and < Y -p, V> = 0.
Using p = aU + bV in both equations gives us this system:
a< U, U> + b< V, U> = < Y, U>
a< U, V> + b< V, V> = < Y, V> .
a + 2b = -0.782
2a + 6b = -2.266
Solving this system gives us a = -0.0800 and b = -0.3510.
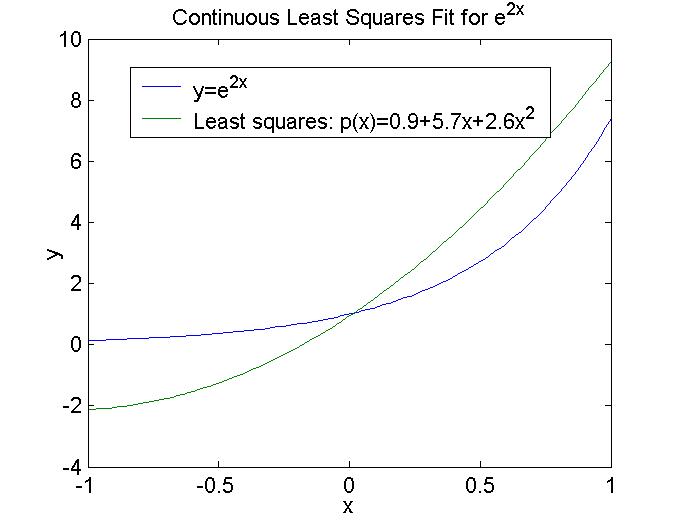
Solution This problem is really a straightforward application of the minimization results we got earlier. The inner product is the one found in Example 11 on p. 166 of the text. The normalized Legendre polynomials of degree 0, 1, and 2 are found at the bottom of p. 166. To simplify notation here, we will let
p0(x) = 2-1/2, p1(x) = (3/2)1/2x, and p2(x)= (5/8)1/2(3x2-1).
The polynomial p(x) that minimizes ||f-q|| among all q in P2 is
p(x) = < f, p0> p0(x) + < f, p1> p1(x) + < f, p2> p2(x).
The inner products are all integrals of products of polynomials and exponentials; doing them results in these values:
< f, p0> = 8-1/2(e2 - e-2)
< f, p1> = (3/32)1/2(2e2 + 3e-2)
< f, p2> = (5/128)1/2(e2 - 13e-2)
The final polynomial we get is
p(x) = (1/4)(e2 - e-2) + (3/8)(2e2 + 3e-2)x + (5/32)(e2 - 13e-2)(3x2-1).
Here is the required plot.