Least Squares Problems

  1. (Discrete least squares.) The table below contains data obtained by measuring the concentraion of a drug in a person's blood. Find and sketch the straight line that best fits the data in the discrete least squares sense.

    Log of Concentration
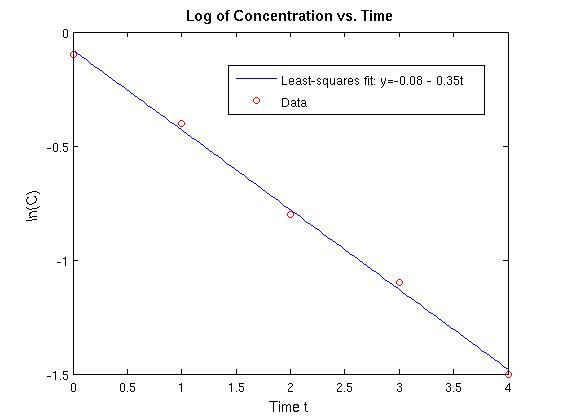
    t  0  1  2  3  4
    ln(C)   − 0.1  − 0.4  − 0.8  − 1.1  − 1.5

    Solution Let u0 = [1 1 1 1 1]T, u1 = [0 1 2 3 4]T, and yd = [-0.1 -0.4 -0.8 -1.1 -1.5]T. To do a least squares straight-line fit y = a0 + a1t to the data, we need to find a0 and a1 such that ||y - a0 u0 - a1 u1|| is a minimum. The norm and inner product are the standard ones for R5. This is equivalent to finding w in span{u0u, 1} that minimizes ||yd - w||. Recall that we showed that there is a unique solution to this problem,

    wmin = < yd | v0> v1 + < yd | v1> v1

    where v0, v1 form an orthonormal basis for span{u0, u1}. To obtain a0 and a1, we first use the Gram-Schmidt process to find the orthonormal set {v0, v1}. Let y0 = u0, and then set
    y1 = u1 - < y0 | u1>/(<y0 | y0>) y0  =  u1 - 2y0  =  [-2 -1 0 1 2]T.
    The vectors y0 and y1 are orthogonal. Dividing by the appropriate norms then yields
    v0 = 5 −½ y0 and v1 = 10−½ y1.
    Using MATLAB we get < yd | v0> = -1.7441 and < yd | v1> = -1.1068. Consequently, the minimizer is
    wmin = - 1.7441v0 - 1.1068v1.
    We now change back to our original basis {u0, u1} using
    v0 = 5-½ u0 and v1 = 10-½ (u1 - 2u0).
    The result is:

    wmin = - 1.7441×5-½ u0 - 1.1068×10-½ (u1 - 2u0) = - 0.08u0 - 0.35u1,

    which yields a0 = -0.08 and a1 = -0.35. The line we want is thus y = - 0.08 - 0.35t.

  2. (Continuous least squares.) Use the orthonormal basis comprising the normalized Legendre polynomials to obtain the quadratic polynomial that gives the best continuous least-squares fit for the function f(x) = e2x on the interval [-1,1]. Sketch both the function and the polynomial that fits it.

    Solution This problem is really a straightforward application of the minimization results we got earlier. The inner product and norm are
    < f | g > = ∫ −11 f(x)g(x)dx and ||f|| = (∫ −11 f(x)2dx)½.
    As we saw in class, the normalized Legendre polynomials of degree 0, 1, and 2 are

    p0(x) = 2-1/2,   p1(x) = (3/2)1/2x,   and   p2(x)= (5/8)1/2(3x2-1).

    The quadratic polynomial p that minimizes ||f-q|| among all quadratics q is

    p(x) = < f | p0> p0(x) + < f | p1> p1(x) + < f | p2> p2(x).

    The inner products are all integrals of products of polynomials and exponentials; doing them results in these values:

    < f | p0> = 8-1/2(e2 - e-2)
    < f | p1> = (3/32)1/2(e2 + 3e-2)
    < f | p2> = (5/128)1/2(e2 - 13e-2)

    The final polynomial we get is
    p(x) = (1/4)(e2 - e-2) + (3/8)(e2 + 3e-2)x + (5/32)(e2 - 13e-2)(3x2-1).

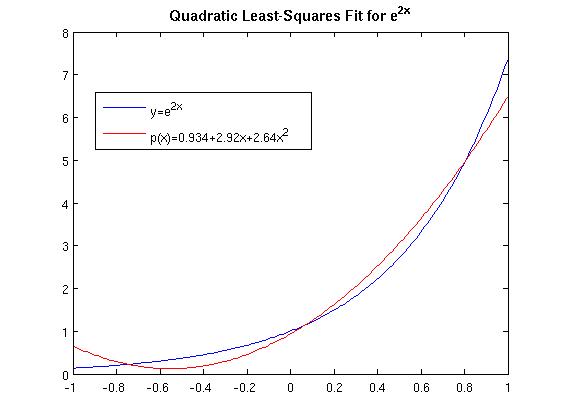
    Here is the required plot.