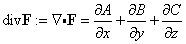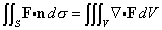Notes on Vector Calculus

Relating line integrals to surface integrals: Stokes's Theorem

The curl and Stokes' Theorem  Let S be a surface in 3D bounded by a simple closed curve C. We will not be absolutely precise here. One should think of S as a butterfly net, with C as its rim. Such a surface is orientable, and we always have a consistent piecewise continuous unit normal n defined on S. We say that C is positively oriented if in traversing C with the surface on our left, we are standing in the direction of n.

To state this theorem, we also need to define the curl of a vector field
F(x)=A(x,y,z)i + B(x,y,z)j +C(x,y,z)k.
We will assume that F has continuous partial derivatives. The curl is then defined by

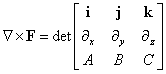
There is a useful physical interpretation for the curl. Suppose that a fluid is rotating about a fixed axis with angular velocity ω. Define ω to be the vector with magnitude ω and with direction along the axis of rotation. The velocity of an element of the fluid located at the position with radius vector x is v(x) = ω×x. With a little work, one can show that ω = ½∇×v. Thus one half of the curl of the velocity vector v is the vector ω mentioned above.

Stokes' Theorem  Let S be an orientable surface bounded by a simple closed positively oriented curve C. If F is a continuously differentiable vector-valued function defined in a region containing S, then

Example  Verify Stokes's Theorem for the vector field F(x) = 2yi + 3xj - z²k over the surface s, where S is the upper half of a sphere x²+y²+z² = 9 and C is its boundary in the xy-plane, the circle x²+y² = 9. C is traversed counterclockwise.

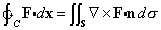
We will first compute the line integral over C. In the xy-plane, C is parameterized via
x(t) = 3 cos(t) i + 3 sin(t) j,   0 ≤ t ≤ 2π,
and so we have:

dx = (- 3 sin(t) i + 3 cos(t) j)dt
F(x(t)) = 2·3 sin(t)i + 3² cos(t)j - 0²k = 2·3 sin(t)i + 3² cos(t)j
F·dx = (- 18 sin²(t) + 27 cos²(t))dt
∫_CF·dx = ∫₀^2π(- 18 sin²(t) + 27 cos²(t))dt = 9π

We now turn to finding the surface integral. ∫∫_S ∇×F·n dσ. The normal compatible with the orientation of C is n = x/|x| = x/3. Thus, on the surface of the hemisphere S, we have
n = x(θ,φ)/3 = (3 sin(θ)cos(φ) i + 3 sin(θ)sin(φ) j + 3 cos(θ) k)/3,
and hence,
n = sin(θ)cos(φ) i + sin(θ)cos(φ) j + cos(θ) k)
where 0 ≤ θ ≤ ½π and 0 ≤ φ ≤ 2π. Also, the area element is dσ = 3²sin(θ)dφdθ. Moreover, it is easy to show that &nabla×F = k. We are now ready to do the surface integral involved:

∫∫_S ∇×F·n dσ = ∫∫_S k·n dσ
∫∫_S ∇×F·n dσ = ∫₀^2π ∫₀^½π cos(θ) 3² sin(θ)dφdθ
∫∫_S ∇×F·n dσ = 9π

Since both terms in Stokes's Theorem have the same value, we have verified the theorem in this case.

Relating surface integrals to volume integrals: the Divergence Theorem

The divergence of a vector field and the Divergence Theorem  The divergence of a vector field F(x)=A(x,y,z)i + B(x,y,z)j +C(x,y,z)k is defined by

Like the curl, the divergence of F has a physical interpretation in terms of fluids. This will be made clearer later. Here is the statement of the Divergence Theorem.

Divergence Theorem  Let V be region in 3D bounded by a closed, piecewise smooth, orientable surface S; let the outward-drawn normal be n. Then,

Example  Verify the Divergence Theorem for the surface integral ∫∫_S F·ndσ, where F = 3xi+yj+2zk and S is the surface of the closed cylinder (including caps) x²+y² = 16, 0 ≤ z ≤ 5. The normal is outward drawn.

To do this we must compute both integrals in the Divergence Theorem. We will first do the volume integral. It is easy to check that ∇·F = 3+1+2=6. Hence, we have that
∫∫∫_V∇·FdV = ∫∫∫_V6dV = 6π·4²·5 = 480π

The surface integral must be broken into three parts: one for the top cap, a second for the curved sides, and a third for the bottom cap.
∫∫_S F·ndσ = ∫∫_top F·ndσ + ∫∫_sides F·ndσ + ∫∫_bottom F·ndσ
The outward normals for the top and bottom caps are k and −k, respectively. For the top (z = 5), we are integrating F(x,y,5)·k = 2·5 = 10, and for the bottom (z = 0), F(x,y,0)·(−k) = −2·0 = 0. Hence, we have
∫∫_top F·ndσ = ∫∫_top 10dσ = 10π4² = 160π
∫∫_bottom F·ndσ = ∫∫_bottom 0dσ = 0
The integral over the curved sides will require a little more effort. The outward normal (see my notes, Surfaces, pg. 5) and area element are, respectively,
n = cos(θ)i + sin(θ)j and dσ = 4dθdz.
In addition, on the curved sides
F(4cos(θ),4sin(θ),z) = 12cos(θ)i + sin(θ)j + 2zk, so F·n = 12cos²(θ) + 4sin²(θ).
The surface integral over the curved sides is then given by
∫∫_sides F·ndσ = ∫₀⁵∫₀^2π (12cos²(θ) + 4sin²(θ))4dθdz = 5·4(12π+4π)= 320π.
Combining these three integrals, we obtain
∫∫_S F·ndσ = 160π+320π + 0 = 480π,
which agrees with the result from the volume integral. Thus we have verified the Divergence Theorem in this case.

Equation of continuity for fluids  Suppose that in a region a fluid has a velocity field v(x,t) and density ρ(x,t), and that there are no sources or sinks in the region. Recall that last class we showed that the amount of fluid crossing a surface in the direction n per unit time is the flux,
Φ = ∫∫_Sρv·ndσ.
If S is a closed surface forming the boundary of a volume V, then Φ is the negative of the total rate of change of mass in the fluid in V. Thus, we have the equation
∫∫_Sρv·ndσ = − d/dt ∫∫∫_VρdV = − ∫∫∫_V∂ρ/∂t dV.
If we use the divergence theorem to replace the surface integral by a volume integral, we obtain
∫∫∫_V ∇·(ρv)dV = − ∫∫∫_V∂ρ/∂t dV,
and, consequently, that
∫∫∫_V (∇·(ρv)+∂ρ/∂t) dV = 0
holds for every choice of V within the region under consideration. If we take V to be a small sphere of radius ε and center x, then the limit as ε tends to 0 of
V^-1∫∫∫_V (∇·(ρv)+∂ρ/∂t) dV
is ∇·(ρv)+∂ρ/∂t. On the other hand, this limit is of course 0. Therefore,
∇·(ρv)+∂ρ/∂t = 0.
This partial differential equation is called the equation of continuity.