- Chapter 0, exercises: 3, 10, 11, 12, 13, 15, 28
- Use the inner product in Example 0.3, pg. 4. Find the projection
of w onto v, where the vectors are displayed
below. Verify that if p is the required projection,
then q := w − p is orthogonal
to v.
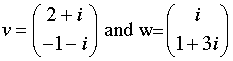
-
Use the L2 inner product given in Definition 0.5, pg. 6,
with a = 0 and b = 1. Let f(x) = x2 and g(x) = x+1. Find
the projection of g onto f. Verify that if p is the required
projection, then q:= g − p is orthogonal to f.
- Use the L2 inner product given in Definition 0.5, pg. 6, with a = −1 and b = 1. Find the straight line y = A+Bx that best fits the function f(x) = ex/2 in the L2[−1,1] sense.