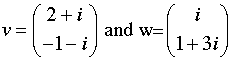Math 414-501 — Spring 2015

Assignment 1 - Due Friday, 1/30/2015.

• Read sections 0.1-0.5, 0.7.1
• Problems.
  1. Chapter 0: 2 (Do Example 0.3, p. 4.), 3, 10, 11, 12, 13, 15, 28
  2. Use the inner product in Example 0.3, pg. 4. Find the projection of w onto v, where the vectors are displayed below. Verify that if p is the required projection, then q := w − p is orthogonal to v.

     

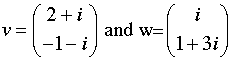
• Point distribution:   1. Text problems, chapter 0:   3 -- 15 pts. (If they only do positivity, give them full credit.) 12 -- 25 pts. 15 -- 20 pts. 28 -- 20 pts.   2. 20 pts. Total = 100 pts.

Assignment 2 - Due Friday, 2/6/2015.

• Read sections 1,1-1.1.3, 1.2.1-1.2.5
• Problems.
  1. Chapter 0: 14 ¹, 17, 23

  2. Chapter 1: 1

  3. Let $V$ be an inner product space and let $V_0$ be a finite dimensional subspace of $V$. Show that if $v\in V$ has $v_0 = \text{proj}_{V_0}(v)$, then \[ \| v - v_0\|^2 = \|v\|^2 - \|v_0\|^2. \]

  4. Let V be a vector space with a complex inner product < ·,· >. Suppose that the set B = {u₁, u₂, ..., u_n} is an orthonormal basis for V.
     1. Re-do the proof we did in class on 1/30/15. That is, show that if
        v = a₁u₁ + a₂u₂ + ... + a_nu_n and w = b₁u₁ + b₂u₂ + ... + b_nu_n,
        then <v, w > = ∑_j a_j b_j = b^T a. (Hint: Put the expression for v in the inner product and then use activity and homogeneity. Finally, identify the coefficients that multiply the a's in the resulting sum.)

     2. Verify this identity in $V=L^2[-1,1]$, where $B$ is the set of orthonormal Legendre polynomials, \[ p_0(x)=\frac{1}{\sqrt{2}}, \quad p_1(x) = \sqrt{\frac {3}{2}}\, x, \quad p_2(x)=\sqrt{\frac{5}{8}}(3x^2-1) \] and v, w are replaced by $x-x^2$ and $12+x-3x^2$, respectively.

• Point distribution:   1. Text problems, chapter 0. 14 -- 25 pts. (Give 9 pts. for the plots.) 23 -- 15 pts. 2. Text problem, chapter 1. 1 -- 25 pts. (Give 12 pts. for the plots.) 3. 5 pts. 4. (a) 15 pts. (b) 15 pts. Total = 100 pts.

Assignment 3 - Due Friday, 2/13/2015.

• Read sections 1,3.1-1.3.4
• Problems.
  1. Chapter 1: 4, 7, 8 (do only n=5 and n = 10), 10

  2. Suppose that f and f′ are continuous 2π-periodic functions. If the Fourier series for f and f′ are
     f(x) = a₀ + ∑_n a_ncos(nx) + b_nsin(nx) and   f′(x) = a′₀ + ∑_n a′_ncos(nx) + b′_nsin(nx),
     then show that the coefficients of the two series are related this way for n ≥ 1:
     a′_n = n b_n, b′_n = − n a_n and a′₀ = 0.
     (Hint: Integrate by parts.) If f is k times continuously differentiable, use induction to derive a similar formula for the the Fourier coefficients of f^(k).

  3. Let $f(x) = \frac{1}{12}(x^3 - \pi^2x)$, $-\pi \le x \le \pi$. In the text (cf. Example 1.9), we derived the Fourier series for $g(x) = x$ on $-\pi \le x <\pi$. Use the series for $g$ and the results from the previous problem to show that the Fourier series for $f(x) = \frac{1}{12}(x^3 - \pi^2x)$ is given by \[ f(x) = \sum_{n=1}^\infty\frac{(-1)^n}{n^3} \sin(nx) \]
• Point distribution:   1. Text problems, chapter 1. 7 -- 10 pts. 10 -- (a) 20 pts. (b) 20 pts. (c) 20 pts. 2. 10 pts. 3. 20 pts. Total = 100 pts.

Assignment 4 - Due Wednesday, 2/18/2015.

• Read sections 1.3.4-1.3.5
• Problems.
  1. Chapter 1: 11¹ (Plot=sketch by hand.), 21, 23(a,b,c) (Plot=sketch by hand; note that the functions have period = 2 and are defined on $-1 \le x \le 1$.), 33
  2. In the previous assignment you showed that \[ \frac{1}{12}(x^3 - \pi^2x) = \sum_{n=1}^\infty\frac{(-1)^n}{n^3} \sin(nx), \ -\pi \le x \le \pi. \] Use this formula and Parseval's equation to find the sum of the series $\sum_{n=1}^\infty \frac{1}{n^6}$.
• Point distribution: 1. Text problems, chapter 1. 11 -- (a) 20 pts. (b) 20 pts. 21 -- (a) 5 pts. (b) 20 pts. 23 -- (a) 5 pts. (b) 5 pts. (c) 5 pts. 33 -- 10 pts. 2. 10 pts. Total = 100 pts.

Assignment 5 - Due Friday, 2/27/2015.

• Read sections 1.3.1, 1.3.2, 2.1 and 2.2.
• Problems.
  1. Chapter 1: 32(a,c,d,e,f)
  2. Chapter 2: 1, 2, 4.
  3. Find the Fourier transform of $f(t) = e^{-|t|}$. In addition, use this transform and the properties listed in Theorem 2.6 to find the Fourier transforms of the following functions:

     1. $t e^{-|t|}$ (Use #2.)

     2. $e^{-2|t-3|}$ (#6 and #7)

     3. $\text{sgn}(t)e^{-|t|}$ (Hint: differentiate $e^{-|t|}$; use #4.) Here, $\text{sgn}(t) = \begin{cases} 1 & t > 0,\\ 0 & t = 0, \\ -1 & t < 0.\end{cases} $

     4. $\frac{1}{1+(t-2)^2}$  (Hint: How are Fourier transforms and inverse Fourier transforms related? Use the answer to this and #6)

  4. Find the Fourirer transforms of these functions.
     1. $g(t)=\begin{cases}1 & -1 \le t \le 2, \\ 0 & \text{otherwise}. \end{cases}$

     2. $h(t) = \begin{cases} 1 & 0 \le t \le 1,\\ -1 & -1 \le t < 0 \\ 0 & \text{otherwise.} \end{cases} $
• Point distribution: 1. Chapter 1. 32 -- (a) 10 pts. (c) 10 pts. (f) 10 pts. 2. Chapter 2. 2 -- 15 pts. 3. (a) 15 pts. (c) 10 pts. (d) 15 pts. 4. (b) 15 pts. Total = 100 pts.

Assignment 6 - Due Monday, 3/9/2015.

• Read sections 2.3 and 2.4.
• Problems.
  1. Chapter 2: 5, 6.
  2. Let $\phi(t) := \begin{cases} 1 & 0 \le t < 1, \\ 0 & \text{otherwise},\end{cases}$ and $\psi(t) := \begin{cases} 1 & 0 \le t < 1/2, \\ -1 & 1/2 \le t <1, \\0 & \text{otherwise.}\end{cases} \ $ Find $\phi\ast \psi(t)$.
  3. Let $h(t) = \begin{cases} 1 & -\pi \le t < \pi , \\ 0 & \text{otherwise}. \end{cases} \ $ Recall that $\hat h(\lambda) = \sqrt{\frac{2}{\pi}} \frac{\sin(\pi \lambda)}{\lambda} $. Use Plancheral's theorem to find $\int_0^\infty \frac{\sin^2(x)}{x^2}dx$.

  4. Suppose that $f(t)=0$ for all $|t| \ge a >0$ and $g(t) = 0 $ for all $|t| \ge b > 0$. Show that $f\ast g(t) = 0$ for all $|t| \ge a+b$.

  5. Let f(t) be a signal that is 0 when t < 0 or t > 1. Show that, for the Butterworth filter, one has

     L[f] = A e^{− α t} ∫ ₀^min(1,t) e^ατ f(τ)dτ, if t ≥ 0, and that L[f] = 0 if t < 0.

• Point distribution: 1. Chapter 2, problem 6 -- 20 pts. 2. 20 pts. 3. 20 pts. 4. 20 pts. 5. 20 pts. Total = 100 pts.

Assignment 7 - Due Wednesday, 3/25/2015.

• Read section 3.1.
• Problems.
  1. Chapter 2: 8, 13.

  2. This is a version of problem 12, chapter 2. Take $h(t)$ to be the function defined in that problem.
     1. Show that the Filter has the form $L[f] = \frac{1}{d} \int_{ t - d}^t f(\tau)d\tau$.

     2. Find $\hat h(\lambda)$. Make the plots required in problem 12, but use $|\hat h(\lambda)|$ rather than $\hat h(\lambda)$. (Interpret cycles/$2\pi$ as a $\lambda$.)

     3. For $t \ge 0$, let $g_\beta(t) = e^{-t} \sin(\beta t)$, where $\beta$ is a real number, and for $ t < 0$, let $g_\beta(t) = 0$. Find $h\ast g_\beta(t)$ for all $t \ge 0$. (Be aware that the cases $0 \le t < d$ and $d \le t$ have to be treated differently.)

     4. Let $f$ be as in problem 12. Use your answer to the previous part to write $f$ as a sum of the $g_\beta$'s, and then find $h\ast f$. Make the plots required for $h\ast f$ in problem 12.

  3. Let $h_1$ and $h_2$ be impulse resonse functions for causal filters $L_1[f] = h_1\ast f$ and $L_2[f]=h_2\ast f$. Show that if $h=h_1\ast h_2$ is the impulse response for $L[f]=h\ast f$, then $L$ is causal.

  4. Recall that we have defined the Gaussian $f_s$ by $f_s(t) = \sqrt{s} e^{-s t^2}$ and shown that $\hat f_s(\lambda) = \frac{1}{\sqrt{2}} e^{-\lambda^2/(4s)}$. (Chapter 2, problem 6.) Consider the two Gaussians $f_3(t) = \sqrt{3}e^{-3 t^2}$ and $f_6(t) = \sqrt{6}e^{-6t^2}$. Show that $f_3 \ast f_6(t) = \sqrt{\pi} f_{2}(t)=\sqrt{2\pi} e^{-2t^2}$.

• Point distribution: 1. Chapter 2: 8 -- 10 pts.; 13 -- 20.   2. (c) 25 pts. (d) 25 pts.   4. 20 pts.   Total = 100 pts.

Assignment 8 - Due Wednesday, 4/1/2015.

• Read sections 3.2.1, 4.2.1, 4.2.2.
• Problems.

  1. Suppose that x is an n-periodic sequence (i.e., x ∈ S_n). Show that $ \sum_{j=m}^{m+n-1}{\mathbf x}_j = \sum_{j=0}^{n-1}{\mathbf x}_j $. (This is the DFT analogue of Lemma 1.3, p. 44.)

  2. Chapter 3: 2 (Hint: use the previous problem.)
  3. Consider the Gaussian function $f_1(t) = e^{-t^2}$. The Fourier transform of this function is $\hat f_1(\lambda) = \frac{1}{\sqrt{2}} e^{-\lambda^2/4}$. Numerically approximate $\hat f_1(\lambda)$ using the FFT, with $f_1$ being sampled over the interval $[-5,5]$ for n = 256, 512, and 1024. Graph $\hat f_1$ and its FFT approximation $\hat f_{ap}$ for these three values of $n$. (For an example of this type of problem, see Approximating the FT with the FFT.)

• Point distribution: 1. 20 pts.    2. Chapter 3: 2 (Four parts: (i) shifts -- 10 pts. (ii) convolution -- 20 pts. (iii) convolution theorem -- 20 pts. (iv) relation for "y hats" -- 10 pts.)   3. 20 pts. (The graphs in this problem should be labeled. Each plot should have n, FT_actual and FT_approx. Take off two points if there were no labels.) Total = 100 pts.

Assignment 9 - Due Friday, 4/10/2015.

• Read sections 4.2-4.4.
• Problems.
  1. Chapter 3: 16.
  2. Let $x_j = \begin{cases} 1, & 0 \le j \le N-1, \\ 0, & \text{otherwise}. \end{cases}$ Show that $ \hat x(\phi) = \frac{e^{-i\frac{N-1}{2}\phi}\sin\big(\frac{N}{2}\phi\big) }{\sin\big (\frac12 \phi\big)} $.
  3. Let $x = (\cdots x_{-2}\ \ x_{-1}\ \ x_0 \ \ x_1 \ \ x_2 \ \ x_3 \cdots )$ be in $\ell^2$ and let $y = T_p(x)$. Show that the Z-transforms of $x$ and $y$ are related by $\hat y(\phi) = e^{-ip\phi}\hat x(\phi)$.
• Start putting together groups for projects.
• Point distribution: 1. Chapter 3: 16, 30 pts.    2. 35 pts.    3. 35 pts. Total=100 pts.

Assignment 10 - Due Wednesday, 4/15/2015.

• Read sections 4.2-4.4.
• Problems.
  1. Chapter 4: 1. Do this problem by the method in Example 4.11. Sketch this by hand.
  2. Chapter 4: 2. Do this problem by using the formulas in Theorem 4.12 to find the coefficients, and then the component parts. Sketch this by hand.
  3. Chapter 4: 6, 7. Do the sketches by hand.
  4. Show that $a^j_k = 2^{\frac{j}{2}}\int_{-\infty}^\infty f(x)\phi_{j,k}(x)dx =2^{j}\int_{-\infty}^{\infty} f(x)\phi(2^jx - k)dx$. (This is an easy problem. Use Theorem 0.21, p. 17, along with the fact that $\{\phi_{j,k}\}_{k\in \mathbb Z}$ is an orthonormal basis for $V_j$.)
• Start putting together groups for projects.

Assignment 11 - Due Monday, 4/27/2015.

• Read sections 5.1 and 5.2.
• Form a group (2-4 is OK) and choose someone to represent the group. Pick a topic for the project. The reprentative should email me a list of the members and a short explanation of the topic.