Math 601 - Fall 2000

Homework

Assignment 11

Problem 7.5, pg. 205-206 in Zachmanoglou and Thoe (Z/T).
Problems 7.7(a,b), pg. 205-206 in Z/T
Problem 8.10(a), pg. 221 in Z/T.
Problem 8.10, pg. 317 in Z/T.

Due Thursday, Nov. 30.

Assignment 10

Verify Stokes' Theorem

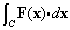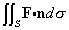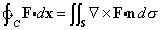
for F(x) = 2y i - 3z j + x k, with S being the part of the sphere x²+y²+ z² = 4 in the first octant. The normal to S points away from the origin, and C is the positively oriented curve that serves as the boundary of S.
Verfiy the Divergence Theorem

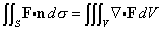
for F(x) = 2y i + 3x j - z³ k, with S being the surface of the closed cylinder (top, bottom, and curved side) 0 <= z <= 2, x² + y² = 25, with outward drawn normal. (This is the same cylinder as in Problem 4(b), Assignment 9.)

Due Tuesday, Nov. 21.

Assignment 9

Compute the line integral

for the following vector fields and curves.
1. F(x) = (3x-4y)i + (y²+2x)j, where C is the straight line from (0,1) to (1,1) followed by the straight line from (1,1) to (1,2).
2. F(x) = (3x-y)i + (x+y)j, where C is the circle x²+y² = 4 traversed once in the positive (counterclockwise) direction.
3. F(x) = (3x²+2y)i + (y-3x)j, where C is the straight line from (1,1) to (2,3).
4. F(x) = (3x+y-z)i + (zx-xy²)j + 3xyz k, where C is the curve parametrized by x=t, y=t², z=-t, for t=0 to t=2.
Calculate the standard normal for the surface S parametrized by x = u i + v j + f(u,v)k, where R_uv is the rectangle a <= u <= b, c <= v <= d. Find an expression for area of S.
Consider a surface parametrized by x = x(u¹, u²). Let f₁, f₂ be the partials of x with respect to u¹, u². Show that the metric tensor is given by g_jk = f_j· f_k, and use this to show that det(g)^1/2 = |N|, where N is the standard normal.
Compute the flux integral

for the following vector fields and surfaces.
1. F(x) = 3z i + 2x j + y k, where the surface S is the upper half of the hemisphere x²+y²+ z² = 9; the normal direction is upward.
2. F(x) = zx i - 2xyz j + z² k, where the surface is the curved part of the cylinder x²+y² = 25, with 0 <= z <= 2. Take the normal as pointing away from the z-axis.

Due Thursday, Nov. 16.

Assignment 8

Let V be ordinary three dimesional space, with the usual ``dot'' and ``cross'' products · and ×. Let the set F={f₁, f₂, f₃} be a (possibly) nonorthogonal basis for V. Show that the dual basis F*={f¹, f², f³} satisfies
f¹ = r f₂×f₃
f² = r f₃×f₁
f³ = r f₁×f₂,
where r = (f₁ · f₂×f₃)^-1. What is the geometrical significance of r^-1?
Consider the tetrahedron with vertices (0,0,0), (a,0,0), (0,b,0), (0,0,c). Let A and n be the area and normal for the inclined face, and let A_j be the area of the face with outward normal -e_j.
1. Show that A n = A₁e₁ + A₂e₂ + A₃e₃
2. Show the volume of the tetrahedron is proportional to A^3/2, and so the the ratio of volume to A tends to 0 as A tends to 0.
Derive this formula for the strain tensor. (For notation, see the summary for 2 November.)
s_j,k = ½(D_xju^k + D_xku^j + SUM_i D_xjuⁱD_xkuⁱ)
Metric tensor. Show that, if we change from cartesian coordinates x to general coordinates w, the metric tensor becomes
g_j,k = SUM_i D_wjxⁱ D_wkxⁱ
Find the metric tensor for spherical and cylindrical coordinates.

Due Thursday, Nov. 9.

Assignment 7

Consider the matrix:

A = 1 -1

1 -1.001
1. Find the SVD for A.
2. For a square matrix, the ratio of the largest to smallest singular values is called the condition number of the matrix. Find the condition number for A.
3. Suppose that û is the measure or calculated estimate of a vector u. The relative error is then
  r_err(u) = || û - u ||· || u ||^-1.
  Solve the systems Au = [1 1]^T and Aû = [0.999 1.001]^T exactly. Calculate r_err(u). How does this compare with the relative error in the right hand side, which is 0.001? How does the ratio of r_err(u) to 0.001 compare with the condition number for this problem? Briefly explain your results.
Find the LU decomposition for the matrix:

B = 1 4 7

2 5 8

3 6 10
Find the Jacobian derivative f´ for the function
f(u,v)=(sin(u)cos(v),sin(u)sin(v),cos(u))^T.
Suppose that g and h are inverse functions, so that g(h(u)) = u and h(g(w)) = w. Use the chain rule to verify that
h´(u) = g´(w)^-1, where u = g(w) and w = h(u).
Consider the nonlinear change of coordinates x = g(u) in R²:
(x,y)^T = (u+v, u² - v)^T.
Let R_uv be the triangle in the u-v plane bounded by u = 0, v = 0, and u+v=2. Find the region R_xy in the x-y plane that is the image of R_uv under g. On this region, find the function inverse to g.

Due Thursday, Nov. 1.

Assignment 6

Find the eigenvalues and eigenvectors of the matrices below. Determine whether or not a given matrix is diagonalizable. If it is, find S for which S^-1AS=D.
```
 3  4        2  1 
-1 -1       -1  2 

 4 -1  1
-1  4 -1
 1 -1  4
```
Partitioning/block multiplication of matrices A, B. A column partition of A must match the row partition in B One can then multiply blocks in the same way as ordinary elements, except that the order of blocks must be preserved - A then B.
1. Let A be the matrix below, and let B be a matrix with 6 rows, partitioned 1 2 | 3 4 5 | 6 . Give two block partitions for A compatible with B's partitioning scheme. How many partitions are there for A that are compatible with B?
```
-2  1  5  1  2  3
 0  4  9 -1 -6  4
 1 -3  7  0  1 -8
 5  1 -1  1  5  3
```
2. Use partitioning to show that if R is an invertible m×m matrix, and I is the r×r identity, then the matrix S given by
```
I 0
0 R
```
  is invertible and has inverse
```
I 0
0 R^-1.
```
3. Use block multiplication to show that if A has the structure
```
U V
0 W,
```
  where U is an r×r upper triangular matrix, V is an r×m matrix, W is an m×m, and 0 is the m×r zero matrix, then S^-1A S has the same structure.
Triangularization of a matrix. Let A be an n×n matrix, and let z₁ be an eigenvalue of A.
1. Show that there is a matrix R such that R^-1A R =
```
z₁ *
0 A₁
```
  where A₁ is (n-1)×(n-1).
2. Repeat this procedure with the matrix A₁, which will have an eigenvalue z₂. Use the results of part (a) and of the last problem to show that there is a matrix S₁ for which S₁^-1A S₁ =
```
z₁ * *
0 z₂ *
0 0 A₂.
```
3. Continue the procedure and show that there is a matrix S for which S^-1A S is upper triangular, with diagonal elements z₁, z₂,..., z_n. We assumed that z₁ was an eigenvalue of A. Explain why the others are as well. Show that if an eigenvalue z_j is repeated m_j times in the list, in the list, then the factor (z-z_j) is repeated m_j times in the characteristic polynomial of A.
Use the procedure sketched in problem 3 to triangularize the matrix
```
 5 1 4
 0 2 0
-1 1 1
```

Due Thursday, Oct. 12.

Assignment 5

Second finite element problem: -y" + y = x, y(0) = y(1) = 0.
1. Find the exact solution.
2. Define the inner product < u,v > = S₀¹(u' v' + u v)dx. Go through the derivation given in the summary for 19 September, and repeat it (with appropriate changes) to show that if we use the norm from the inner product above, the normal equations are Ac = d, where
  A_jk = < w_k, w_j > and d_j = S₀¹ x w_j(x) dx, j=1 ... n-1, and w_j = B(n x - j).
3. Find d_j.
4. Find A_jk.
5. Numerically solve Ac = d for n = 10 and 50. On the same set of axes, plot the exact solution y and, for each n, the minimizer u*, which is our approximation to the solution y.
Let L : P₂ - > P₂ be given by L[p] = ((1-x²)p')' and let B = {1, x, x²} and D = {1 - x, x², x + 1}.
1. Find the change of basis matrix S_{B - > D} that takes coordinates relative to B into ones relative to D.
2. Directly find M, the matrix of L relative to B, and then calculate N, the matrix of L relative to D via
  N = SMS^-1
3. Find the eigenvalues and eigenvectors of L by means of finding the ones for M and transforming back.
Suppose that a linear transformation T : V -> V leaves U = span{v₁, v₂} invariant. If B = {v₁, v₂, v₃, v₄} is a basis for V, verify that the matrix M_T for T relative to B has the structure
```
x x x x
x x x x
0 0 x x
0 0 x x
```
where the x's indicate possible nonzero entries.
Find the eigenvalues and eigenvectors for the matrix A given by
```
1 1 1
0 1 1
0 0 1
```

Due Thursday, Oct. 5.

Assignment 4

Let V be an inner product space, and let S = {w₁, ... , w_n} be a set of vectors in V. Consider the n×n Gram matrix A with entries given by
A_jk = < w_k, w_j >
for j,k=1...n. Show that A is invertible if and only if S is linearly independent.
Finite element problem. (For notation, see the summary for 19 September.)
1. If f(x) = x², find the exact solution to the problem -y'' = f(x), y(0) = y(1) = 0.
2. Recall that the basis element w_j(x) = B(n x - j). Find the d_j's,
  d_j = S₀¹ f(x) w_j(x) dx, j=1 ... n-1.
3. Show that A_jk = < w_k, w_j >, the j-k entry in the Gram matrix for the problem, satisfies
  A_j,j = 2n, j = 1 ... n-1
  A_j,j-1 = - n, j = 2 ... n-1
  A_j,j+1 = - n, j = 1 ... n-2
  A_j,k = 0, all other possible k.
  For example, if n=5, then A is
```
10  -5   0   0
-5  10  -5   0
 0  -5  10  -5 
 0   0  -5  10
```
4. Numerically solve Ac = d for n = 10, 25, 50. On the same set of axes, plot the exact solution y and, for each n, the minimizer u*, which is our approximation to the solution y.
Plot the unit ``circle'' in R² in the p-norm for p = 1, 4/3, 2, 4, and infinity.
Fix a vector a in R³. Find the matrix associated with the linear transformation L: R³ -> R³ defined via the cross product, L[x} = a×x. Use the standard basis, e₁ = i, e₂ = j, and e₃ = k

Due Thursday, Sept. 28.

Assignment 3

Use the Gram-Schmidt process on the polynomials {1,t,t²} in the inner product
< f, g > := _-1S¹ f(t) g(t)dt
to get the (normalized) Legendre polynomials below. What is the matrix R in this case?
p₀(t)=(1/2)^½
p₁(t)=(3/2)^½t
p₂(t)= (5/2)^½(½)(3t² - 1)
Consider the function f(x)=exp(-x) on the interval [-1,1].
1. Use the Legendre polynomials to find the best least-squares quadratic fit to exp(-x) on the interval [-1, 1]. (The coefficient of the polynomial p_k(x) is < f, p_k >.)
2. On the same set of axes, sketch exp(-x), the least-squares fit you've found, and the quadratic Taylor polynomial about x=0 for exp(-x).
Find the QR factorization for the matrix A given below. (Hint: Use the Gram-Schmidt process on the columns of A, with the inner product being < u, v > := v^Tu .)
```
1  -1   2
1   2  -1
0   1   1
2   1   1
```
Show that every set of nonzero, orthogonal vectors is linearly independent.

Due Thursday, Sept. 21.

Assignment 2

In each of the following cases, find the matrix A for which
[v]_D=A[v]_B
1. B={1, 2x, 4x²-1} and D={1, x, x²-1}
2. B={(1,0,0)^T, (0,1,0)^T, (0,0,1)^T} and D={(1,0,-1)^T, (1,1,1)^T, (-1,2,1)^T}
Let B = {v₁ ... v_n}, D = {w₁ ... w_n}, and E = {u₁ ... u_n} be bases for a vector space V. Suppose that you are given these column matrices:
A₁ = [ [v₁]_E ... [v_n]_E]
A₂ = [ [w₁]_E ... [w_n]_E]
The columns of A₁ and A₂ are the E-coordinates of the bases B and D, repectively. Show that
A₁[v]_B = A₂[v]_D, .
where v is an arbitrary vector in V. Use this result to verify that if the two ordered bases are B = {1,x,x²} and D = {(3-x)², x+2, x-1}, then the matrix that takes coordinates relative to B into ones relative to D is
```
  0      0    1
 1/3    1/3  -1
-1/3    2/3  2 1/3;
```
Hint: Take E=B.
Show that, in Schwarz's inequality, one gets equality if and only if u and v are parallel. (Assume u,v are not 0.)
Verify that < f,g > = integral of f(t)g(t) from t=-1 to t=1 defines an inner product on C[-1,1], the set of all functions continuous on [-1,1]. State both the triangle inequality and Schwarz's inequality for this case. Find the angle between the polynomials p(x)=1+x and q(x)=x²

Due Thursday, Sept. 14.

Assignment 1

Verify that the set of all twice continuously differentiable solutions to the wave equation u_tt- u_xx=0 is a subspace of C⁽²⁾(R²).
Let P_n be polynomials of degree n or less in x.
1. Show that P₂ is a subspace of P₃
2. Let U be the subset of P_n comprising all polynomials such that p(1)+p'(1)=0 and p(2)=0. Is U a subspace? What happens if the condition is changed to p(1)+p'(1)=0 or p(2)=0?
Let V be a vector space, and let dim(V) = n. Show that the following are true. (You are given that every basis for V has the same number of vectors in it.)
1. Let C = {v₁ ... v_k}, with k < n. If C is linearly independent, we may add vectors to it to turn it into a basis for V.
2. If U is a subspace of V, then dim(U) is at most n. If dim(U) = n, then U = V.
The span of the columns of an m×n matrix A is called the column space of A. Look up an algorithm for finding a basis for the column space; apply it to the matrix A below.

1 -2 3 3

2 -5 7 3

-1 3 -4 3

Due Thursday, Sept. 7.

A	=	1	-1
		1	-1.001