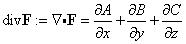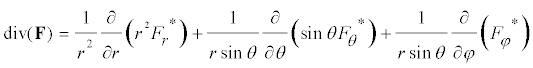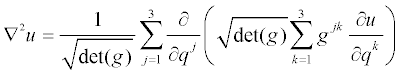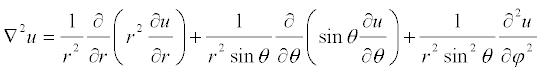- Definition - Vector space. A vector space is a set V
together with two operations, + and · . If u, v are in
V, then u + v is in V; if c is a scalar, then c·v is in
V. The operations satisfy the following rules.
Addition Scalar multiplication u + (v + w) = (u + v) + w a·(b·u) = (ab)·u Identity: u + 0 = 0 + u = u (a + b)·u = a· u + b·u Inverse: u + (-u) = (-u) + u = 0 a·(u + v) = a·u + a·v u + v = v + u 1·u = u
- Definition - Subspace. A nonempty subset U of V is a
subspace if, under + and · from V, U is a vector space
in its own right.
- Theorem. U is a subspace of V if and only if these hold:
- 0 is in U.
- U is closed under + .
- U is closed under · .
- Example: U={(x1, x2, x3) | 2x1 + 3x2 - x3 = 0} is a subspace of R3. On the other hand, W={(x1, x2, x3) | 2x1 +3x2 - x3 = 1} is not a subspace of R3, because 0 is not in W.
- Theorem. U is a subspace of V if and only if these hold:
- Displacements in space, forces, velocities, accelerations, etc.
- + parallelogram law
- · usual scalar multiplication
- Rn (real scalars) or Cn (complex scalars) - n×1 real or complex matrices (i.e., columns; can also work with rows).
- + component of sum is sum of components
- · multiply each component by the scalar
- Pn = {a0 + a1 x + a2x2 + ... + anxn }, the polynomials of degree n or less.
- + polynomial addition
- · multiply each term by the scalar
- Spaces of functions f : X -> scalars, where X can be anything. Think of f(x) as the ``x component of f.''
- + is given by (f+g)(x) = f(x) + g(x) (``component of sum is sum of components'')
- · is given by (c·f)(x) = c(f(x)) (``multiply each component by the scalar'')
- Various subspaces of the vector spaces of the type f : X -> scalars
- C[a,b], all functions continuous on the interval [a,b]. (Could be complex valued).
- C(k)[a,b], all continuous functions having derivatives continuous through order k.
- Definition - Linear combination. Let v1 ...
vn be vectors in a vector space V. A vector of the form
c1v1 + ... + cn vn is
called a linear combination of the vj's.
- Definition - Span. Let S={v1 ... vn} be a subset of a vector space V. The span of S is the set of linear combinations of vectors in S. That is,
U=span(S)={c1v1 + ... + cn vn},
where the cjs are arbitrary scalars.- Proposition. The set span(S) is a subspace of V.
- Examples.
- The polynomials of degree n or less, Pn = span{1, x, x2, ..., xn }
- The set of 3D displacements = span{ i, j, k}
- The set of solutions to y'' + y = 0 is span{ sin(x), cos(x) }.
- U={(x1, x2, x3) | 2x1 + 3x2 - x3 = 0} = span{ (1,0,2), (0,1,3) }. In addition, we also have U = span{ (1,-1,-1), (1,2,7), ((2,-1,1) }.
- Terminology If a vector space V = span(S), we say that V is spanned by S, or V is the span of S, or S spans V.
- Definition - Span. Let S={v1 ... vn} be a subset of a vector space V. The span of S is the set of linear combinations of vectors in S. That is,
- Definition - Linear independence and linear dependence. We
say that a set of vectors
S = {v1, v2, ... , vn}
is linearly independent (LI) if the equation
c1v1 + c2v2 + ... + cnvn = 0
has only c1 = c2 = ... = cn = 0 as a solution. If it has solutions different from this one, then the set S is said to be linearly dependent (LD).- Examples.
- {1, x, x2, ..., xn } is linearly independent.
- {1 + x, 1 - x, 1} is linearly dependent.
- { i, j, k} is linearly independent.
- { (1,0,2), (0,1,3) } is linearly independent and { (1,-1,-1), (1,2,7), ((2,-1,1) } is linearly dependent.
- Any set of three vectors in R2 is linearly dependent.
- Inheritance properties of LI and LD sets. Every subset of a linearly independent set is linearly independent. Every set that contains a linearly dependent set is linearly dependent.
- Examples.
- Classification of vector spaces. If a vector space V has no
limit to the size of its linearly independent sets, it is said to be
infinite dimensional. Otherwise, V is said to be finite
dimensional. 2D and 3D displacements are finite dimensional
spaces. C[0,1] is infinite dimensional, because it contains {1, x,
x2, ..., xk } for all k.
When V is finite dimensional, its LI sets cannot be arbitrarily large. Suppose that n is the maximum number of vectors an LI set in V can have. A linearly independent set S in V having n vectors in it will be called maximal.
- Proposition. If a vector space V is finite dimensional, then any maximal linearly independent set of vectors
S = {v1, v2, ... , vn}
spans V.- Proof. Add any vector v in V to S to form the new set
{v, v1, v2, ... , vn} This augmented set is LD, because it has n+1 > n vectors in it. Thus we can find coefficients c, c1, c2, ... , cn, at least one of which is not 0, such that
c v + c1v1 + ... + cn vn = 0. There are two possibilities. Either c is 0 or c is not 0. In case c = 0, we have c1v1 + ... + cnvn = 0. The set S is LI, so this implies c1 = c2 = ... = cn = 0. But this means all of the coefficients vanish, contradicting the fact that one of them does not vanish. The only possibility left is that c is not 0. We can then divide by it in our previous equation and rewrite that equation as
v = (- c-1c1)v1 + ... + (- c-1cn)vn .
This shows that S spans V. Our proof is complete.- Definition - Basis. We say that a set of vectors
S = {v1, v2, ... , vn}
in a vector space V is a basis for V if S is both linearly independent and spans V.- Corollary. A linearly independent set is a basis for a finite dimensional vector space if and only if it is maximal.
- Definition - Dimension. The dimension of a vector space V is the maximum number of vectors in an LI set. Equivalently, it is the number of vectors common to every basis for V.
- Proposition. If a vector space V is finite dimensional, then any maximal linearly independent set of vectors
- Coordinates and bases
- Coordinates for a vector space. Assigning coordinates
amounts to providing a correspondence
v <-> (c1, c2, ... , cn)
that is 1:1, onto, and preserves vector addition and scalar multiplication. Consider a basis {v1, v2, ... , vn} for a vector space V. We also assume that the basis is ordered, in the sense that we keep track of which vector is first, or second, etc.- Theorem. Let B={v1, v2, ... , vn} be an ordered basis for a vector space V. Every vector v in V can be written in one and only one way as a linear combination of vectors in B. That is,
v = c1v1 +...+ cnvn where the coefficients are unique.Proof. Since B is a basis, it spans V. Consequently, we have scalars c1, ..., cn such that the representation above holds. We want to show that this representation is unique - i,e,, no other set of scalars can be used to represent v. Keeping this in mind, suppose that we also have the representation
v = d1v1 +...+ dnvn,
where the coefficients are allowed to be different from the ck's. Subtracting the two representations for v yields
0 = (c1 - d1) v1 +...+ (cn - dn) vn. Now, B is a basis for V, and is therefore LI; the last equation implies that c1 - d1 = 0, c2 - d2 = 0, ..., cn - dn = 0. That is, the c's and d's are the same, and so the representation is unique.This theorem gives us a way to assign coordinates to V, for the correspondence
v= c1v1 +...+ cnvn <-> (c1, c2, ... , cn) it sets up is both 1:1 and onto. The condition of linear independence gives us that it is 1:1, and the condition of spanning gives us that it is onto. It is also easy to show that this correspondence preserves addition and scalar multiplication, which are the properties needed in defining "good" coordinates for a vector space.- Definition - Coordinate Vector. Given an ordered basis B = {v1 ... vn} and a vector v = c1v1 +...+ cnvn, we say that the column vector [v]B = [c1, ..., cn]T is the coordinate vector for v, and that c1, c2, ..., cn are the coordinates for v.
- Definition - Isomorphism. Let U and V be vector spaces. A correspondence between U and V
u <-> v
that is 1:1, onto, and preserves vector addition and scalar multiplication is called an isomorphism between U and V, and the two spaces are said to be isomorphic.The word isomorphism comes from two Greek words, "isos," which means "same", and "morphy," which means "form." As far as vector space operations go, two isomorphic vector spaces have the "same form" and behave the same way. Essentially, the spaces are the same thing, just with different labels. For example,a basis in one space corresponds to a basis in the other. Indeed, any property in one space that only involves vector addition and scalar multiplication will hold in the other. This makes the following theorem, which is a consequence of what we said above concerning coordinates, very important.
- Theorem. Every n-dimensional vector space is isomorphic to Rn or Cn, depending on whether the set of scalars is R or C.
- Examples. The space P2 of polynomials of degree 2 or less has B = { 1, x, x2 } as a basis, and so it is three dimensional (B has three vectors). We take the scalars to be real. Relative to this basis, we have
[p]B = [ a1 + a2x + a3x2 ]B = [a1 a2 a3]T. Thus, for example, we have these:
[1-x+x2]B = [1 -1 1]T
[-3x+4-2x2]B = [4-3x-2x2]B = [4 -3 -2]T
[(2-x)2]B = [4-4x+x2]B = [4 -4 1]T Changing the ordering of the basis vectors changes the ordering of the coordinates. Using the basis C = { x2 1, x }, we have
[-3x+4-2x2]C = [-2x2+4-3x]C = [-2 4 -3]T, which is a reordering of the coordinate vector relative to B. Be aware that order matters!This isn't the only isomorphism between P2 and R3. Recall that a quadratic polynomial is determined by its values at three distinct values of x; for instance, x=-1, 0, and 1. Also, we are free to assign whatever values we please at these points, and we can get a quadratic that passes through them. Thus, the correspondence
p <-> [p(-1) p(0) p(1)]T
between P2 and R3 is both 1:1 and onto. It is easy to show that it also preserves addition and scalar multiplication, so it is another isomorphism between P2 and R3. Let's use this to find a new basis for P2. (Remember, a basis in one isomorphic space corresponds to a basis in the other.) Since { [ 1 0 0 ]T, [ 0 1 0 ]T, [ 0 0 1 ]T } is a basis for R3, the set of polynomials
C = { p1(x) = -½x + ½x2, p2(x) = 1, p3(x) = ½x + ½x2 },
which satisfy
p1(-1) = 1, p1(0) = 0, p1(1) = 0,
p2(-1) = 0, p2(0) = 1, p2(1) = 0,
p3(-1) = 0, p3(0) = 0, p1(1) = 1,
is another basis for P2. This raises the question of how the coordinate vectors [p]C and [p]B are related. - Theorem. Let B={v1, v2, ... , vn} be an ordered basis for a vector space V. Every vector v in V can be written in one and only one way as a linear combination of vectors in B. That is,
- Let B = {v1 ... vn} and D =
{w1 ... wn} be ordered bases for
a vector space V. Suppose that we have these formulas for v's
in terms of w's and vice versa:
vj=A1jw1 + A2jw2 + ... + Anjwn
wk=C1kv1 + C2kv2 + ... + Cnkvn
(Note that the sums are over the row index for each matrix A and C.) For any vector v with representations
v = b1v1 +...+ bnvn
v = d1w1 +...+ dnwn
and corresponding coordinate vectors
[v]B = [b1,..., bn]T
[v]D = [d1,..., dn]T
we have the change-of-basis formulas
[v]D = A[v]B and [v]B = C[v]D.
These imply that AC=CA=In×n, so C=A-1 and A=C-1 .For purposes of comparison, we want to write out the expressions for the coordinate changes. Writing the d's in terms of the b's, we have
dk = Ak1 b1 + ... + Akn bn. Going the other way, we can write the b's in terms of the d's,
bk = Ck1 d1 + ... + Ckn dn. We note that quantities transforming according to the formula for bases are called covariant, and quantities transforming like the coordinates are called contravariant.
- R2. Let B={v1=i,
v2=j} and let
D={w1=i - j,
w2=2i + 3j}. Note that we have
w1=v1 - v2
w2=2v1 + 3v2 Hence, we have that C11 = 1, C21 = -1, C12 = 2, and C22 = 3. Consequently,
b1 = d1 + 2d2
b2 = -d1 + 3d2 We remark that the matrix C =1 2 -1 3
and the matrix A = C-1 =3/5 -2/5 1/5 1/5
- Pn. We will consider the n = 2 case. Consider
the two ordered bases,
B = {1,x,x2} and D = {(3-x)2, x+2, x-1}. Because we have
w1 = (3-x)2 = 9 - 6x + x2 = 9v1 - 6v2 + v3
w2 = 2+x =2v1 + v2 + 0v3
w3 = (-1)+x = - v1 + v2 + 0v3, The matrix that takes coordinates relative to D into ones relative to B is C =9 2 -1 -6 1 1 1 0 0
The matrix that takes coordinates relative to B into ones relative to D is A =0 0 1 1/3 1/3 -1 -1/3 2/3 7
- Consider the following system of ordinary differential equations,
relative to x1-x2 coordinates.
dx1/dt = 3x1 + 2x2
dx2/dt = 2x1 + 3x2 We can turn this into a very simple decoupled system if we change from x1-x2 coordinates to the u1-u2 set defined via these equations:
x1 = u1 + u2
x2 = u1 - u2 . Afrter some algebra, the system of ODEs becomes
du1/dt = 5u1
du2/dt = u2 , which can be easily solved.
- Definition - Dual Space. The set V* of all
linear functions L:V - > R (or C) is called
the (algebraic) dual of V. The term linear means that
L(au + bv) = aL(u) + bL(v) holds for all scalars a,b and vectors u, v.- Terminology. Linear functions in the dual space are called linear functionals, to distinguish them from other types of linear functions. They are also called or 1-forms or co-vectors.
- Proposition. V* is a subspace of all functions mapping V to the scalars.
- Proof. We leave this as an exercise.
A simple physical example is the work W done by a force f applied at a point and producing a displacement s. Here, the work is given by W=L(s) = f·s. The point is that is if we fix the force, then the work is a linear function of the displacement. Note that forces and displacements have different units and are thus in different vector spaces, even though the spaces are isomorphic.
Another simple example that frequently comes up is multiplication of a column vector X by a row vector Y. The linear functional in this case is just L(X) = Y X. Our final example concerns C[0,1]. L[f] = 0S1 f(x)dx is a linear functional.
- Terminology. Linear functions in the dual space are called linear functionals, to distinguish them from other types of linear functions. They are also called or 1-forms or co-vectors.
- Let V be an n-dimensional vector space. We want to construct a
basis for V*. Let B = {v1 ...
vn} be a basis for V. We may uniquely write any
v in V as
v = x1 v1+ ...+ xn vn Now, if L is a linear functional (i.e., it is in V*), we also have
L(v) = x1 L(v1)+ ...+ xnL(vn). Thus knowing L(vj) for j=1 ... n completely specifies what L(v) is. Conversely, given scalars {y1, ..., yn}, one can show that
L(v) = x1y1 + ...+ xnyn, where the xj 's are the components of relative to B, defines a linear functional. As before, L(vj) = yj. In summary, we have established this.- Theorem. Let V be a vector space with a basis B = {v1 ... vn}. If L is a linear functional in V*, then
L(v) = x1y1 + ...+ xnyn, where yj = L(vj) Conversely, given scalars {y1, ..., yn}, the formula for L above defines a linear functional in V*, where again L(vj) = yj.We can use the theorem we just obtained to define n linear functionals {v1 ... vn} via
 To make this clearer, let's look at what v1 does to
vectors. If we take a vector v = x1
v1+ ...+ xn vn, then
To make this clearer, let's look at what v1 does to
vectors. If we take a vector v = x1
v1+ ...+ xn vn, then
v1(v) = x1v1(v1) + x2v1(v2) + ... + xnv1(vn) = x1·1 + x2·0 + ... +xn·0 = x1. A similar calculation shows that v2(v) = x2, v3(v) = x3, ..., vn(v) = xn. This means that we can write L(v) = x1y1 + ...+ xnyn as
L(v) = y1v1(v) + ... + ynvn(v)
= (y1v1 + ... +ynvn)(v) Now the two sides are equal for all values of the argument, so they are the same function. That is, L = yjv1 +...+ ynvn. Hence, the set B* = {v1 ... vn} spans V*. The set is also linearly independent. If 0 = yjv1 +...+ ynvn, then 0=0(vj) = yj. Hence, the only yj's that give 0 are all 0. Summarizing, we have obtained this result.- Theorem. If V is an n-dimensional vector space, and if B = {v1 ... vn} is a basis for V, then the dual space V* is also n-dimensional and B* = {v1 ... vn} is a basis for V*.
- Definition - Dual Basis. The basis B* is called the dual basis for B.
- Theorem. Let V be a vector space with a basis B = {v1 ... vn}. If L is a linear functional in V*, then
- Definition - Inner product Let V be a real vector
space. We say that a mapping < , > : V×V --> R is
an inner product for V if these hold:
- positivity - <v,v> > 0, with <v,v> = 0 implying that v=0.
- symmetry - <u,v> = <v,u>
- homogeneity - <cu,v > = c<u,v >
- additivity - < u+v,w> = <u,w> + <v,w>
- Definition - Norm The quantity ||v|| := (<v,v>)½ is called the norm or length of a vector v.
- Schwarz's inequality: |<u,v>| <= ||u|| ||v||.
Schwarz's inequality shows that the quotient |<u,v>| ÷ ||u|| ||v|| is always between -1 and 1. Consequently, we may define an angle between vectors to be cos-1(<u,v>(||u|| ||v||)-1). The norm or length of a vector ||v|| satisfies three important properties.
- positivity - ||v|| > 0, unless v = 0
- positive homogeneity - ||cv|| = |c| ||v||, where c is any scalar.
- The triangle inequality: ||u+v|| <= ||u|| + ||v||
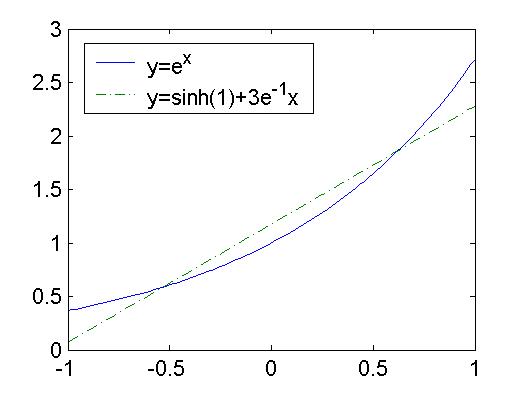
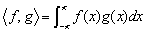 To do the integrals involved, we used the following product-to-sum
trigonometric identities:
To do the integrals involved, we used the following product-to-sum
trigonometric identities:
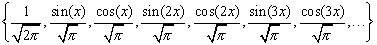
 periodic function f is usually written
as
periodic function f is usually written
as
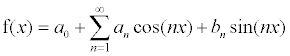 where the coefficients are given by
where the coefficients are given by
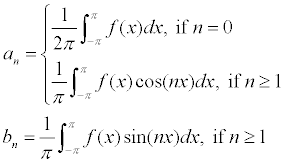 As an example, we calculated the Fourier series for the 2
As an example, we calculated the Fourier series for the 2
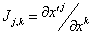 Relative to the primed system, we have a basis B' =
{f1',f2',f3'}. The
new components for the displacement dx are related to the old
via these equations:
Relative to the primed system, we have a basis B' =
{f1',f2',f3'}. The
new components for the displacement dx are related to the old
via these equations:
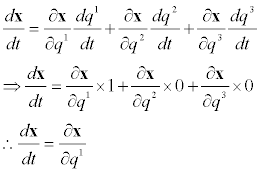 Set t = q1. This gives us our first basis vector,
e1. The others are defined in the same way. That is,
for j=1,2,3, we set
Set t = q1. This gives us our first basis vector,
e1. The others are defined in the same way. That is,
for j=1,2,3, we set
 Together, these form a basis for the 3D displacements. The basis
vectors, however, do depend on the point described by the
coordinates q1, q2, q3. This means
that a different basis is associated with each point in three
dimensional space.
Together, these form a basis for the 3D displacements. The basis
vectors, however, do depend on the point described by the
coordinates q1, q2, q3. This means
that a different basis is associated with each point in three
dimensional space.