Math 642-600 Assignments — Spring 2014
Assignment 1 - Due Wednesday, 1/22/2014.
- Do the following problems.
- Problem 2, page 204 (§ 5.1).
- Problem 7, page 204 (§ 5.1).
- Hanging chain problem. A chain having uniform linear
density ρ hangs between the points (0,0) and (1,0). The total mass
m, which is fixed, and the total energy E of the chain are
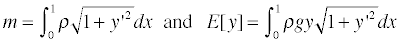 Assuming that the chain hangs in a shape that minimizes the
energy, find the shape of the hanging chain.
Assuming that the chain hangs in a shape that minimizes the
energy, find the shape of the hanging chain.
- Consider the functional J(y) =
∫abF(x,y,y′)dx, where y ∈
C1 and y(a)=A, y(b)=B are fixed.
- Let y extremize J, subject to all of the conditions above. Verify
that if η ∈ C1 and η(a)=η(b)=0,
then
Δ J = ∫ab (-g(x) +
Fy′(x,y,y′))η′(x)dx, where g(x) =
∫axFy(u,y,y′)du.
- Use (a) to show that -g+Fy′(x,y,y′)=c, a
constant. From this, it follows that
Fy′(x,y,y′)∈ C1. (Du
Bois-Reymond, 1879. The point is that one need not assume that
y′′ exists.)
- Smoothing spline. Let J[y] =
∫01 (y′(x))2dx. Let the
admissible set for J be all piecewise C1 curves on [0,1]
that satisfy y(k/n) = yk , for k = 0, 1, 2, ..., n, with
the discontinuities in y′ appearing only at the points
xk = k/n. Use
the previous problem to show that the minimizer for J is a linear
spline passing through all of the points {(xk,yk), k = 0,
..., n}. (Hint: y(x) is in C1[xk,
xk+1]).)
- Let x = (x,y) and let J[x] =
x2y(x2 + y2)− 1
if x ≠ 0, J[0] = 0. Show that the
Gâteaux derivative exists at at x = 0 for every
direction η = (h,k). Also, show that the Fréchet derivative
doesn't exist at x = 0.
Assignment 2 - Due Monday, 2/3/2014.
- Read sections 5.2.1, 5.2.2, and 5.4.
- Do the following problems.
- Problem 10, page 204 (§ 5.1).
- Problem 4, page 205 (§ 5.2).
- Problem 6, page 205 (§ 5.2).
- Problem 7, page 206 (§ 5.2). (Find the Hamiltonian and write
out Hamilton's equations.)
- Problem 8, page 206 (§ 5.2). Also, find the Hamiltonian of
the system, and write out Hamilton's equations for it. Finding
integrals (constants) of the motion should follow immediately from
these equations. (Note: There is an error in the expression for L. The
(dθ/dt)2 sin2θ) should be replaced
by (dφ/dt)2 sin2θ.)
- Find the Legendre transformation H(p) for F(x) =
xT A x, where x is in
Rn and A is a symmetric, positive definite n×n
matrix.
Assignment 3 - Due Monday, 2/17/2014.
- Read sections 6.1 and 6.2.
- Do the following problems.
- Problem 1, page 207 (§ 5.4).
- Problem 4, page 208 (§ 5.4).
- Problem 6, page 208 (§ 5.4). Take Ω to be a 2D disk
centered at 0 and having radius r = a. How does the lowest
eigenvalue change with the radius a?
- Problem 8, page 208 (§ 5.4).
- Use a quadratic polynomial to estimate the lowest eigenvalue for
the Sturm-Liouville problem with Lu = − u′′ =
λu, u(0) = 0, u′(1)+u(1) = 0.
- In class we showed that the Hamiltonian $H=\frac{1}{2m}
(p_r^2+r^{-2}p_\theta^2 - Kr^{-1})$, for a planet (mass $m$) in
orbit around the sun (mass=$M$). The constant $K=GmM$. In addition,
we also found that $H = E$ and $p_\theta = L$ are constants of the
motion.
- Show that $p_r = Lr^{-2} \frac{dr}{d\theta} = -
L\frac{d}{d\theta}(r^{-1})$.
- Let $u = r^{-1}- mKL^{-2}$. Show that $2m EL^{-2} + m^2K^2L^{-4}
= \big(\frac{du}{d\theta}\big)^2 + u^2$. Solve this first order differential
equation for u in terms of $\theta$.
- Use your solution to the previous part to show that the orbit is
an ellipse.
Assignment 4 - Due Wednesday, 2/26/2014.
- Read sections 6.4 and 6.5.
- Do the following problems.
- Problem 3, page 274 (§ 6.1).
- Problem 4, page 274 (§ 6.1).
- Problem 6, page 274 (§ 6.1).
- Problem 6, page 276 (§ 6.2).
- Problem 9, page 276 (§ 6.2).
- Find all of the Laurent expansions for f(z) = ((z2
− 1)(z+2))−1 about z = 0.
Assignment 5 - Friday, 3/7/2014.
- Read section 6.4.
- Do the following problems.
- Problems 19, 22, 26, and 27 in my notes,
Exercises for complex
variables.
- Let $\lambda >0$. Find $F(\lambda) := \int_{-\infty}^\infty
\frac{e^{i\omega x}}{1+x^4}dx$.
Assignment 6 - Due Friday, 4/4/2014.
- Read sections 7.1 and 7.2.
- Do the following problems.
- Problem 2, page 279 (§ 6.5).
- Problem 8, page 280 (§ 6.5).
- Problem 9, page 280 (§ 6.5).
- Problem 10, page 280 (§ 6.5).
- A planet moving around the Sun in an elliptical orbit, with
eccentricity 0 < ε < 1 and period P has time and angle
related in the following way. Let τ = (2π/P)(t −
tp), where tp is the time when the planet is at
perihelion -- i.e., it is nearest the Sun. Let θ be the usual
polar angle and let u be an angle related to θ via
(1 − ε)1/2 tan(u/2) = (1 +
ε)1/2 tan(θ/2).
It turns out that τ = u − ε sin(u). All three
variables θ, u, and τ are measured in radians. They are
called the true, eccentric, and mean anomalies,
respectively. (Anomaly is another word for angle.)
- Show that one may uniquely solve τ = u − ε
sin(u) for u = u(τ), that u is an odd function of τ, and that
g(τ) = u(τ) − τ is a 2π periodic function of
τ.
- Because g is odd and 2π periodic, it can be represented by a
Fourier sine series,
g(τ) = ∑n bn sin(nτ).
Show that bn = (2/n)Jn(nε), n = 1,
2, ..., where Jn is the nth order Bessel
function of the first kind. Thus, we have that
u = τ + ∑n (2/n)Jn(nε)
sin(nτ).
Assignment 7 - Due Tuesday, 4/29/2014.
- Read 10.1-10.3.
- Do the following problems.
- Problem 6(a,c), page 329 (§ 7.2).
- Problem 11(a,c), page 330 (§ 7.2).
- This refers to Problem 7 on the midterm. Show that every f
satisfying the conditions of the problem is band limited, with
Ω ≤ ρ.
- Consider the one dimensional heat equation, ut =
uxx, with u(x,0) = f(x), where − ∞ < x <
∞ and 0 ≤ t x <∞. By taking the Fourier transform in
x, show that the solution u(x,t) is given by
u(x,t) = ∫R K(x−y,t)f(y)dy, K(ξ,t) =
e−ξ2/4t (4πt)− 1/2.
(The function K(x−y,t) is the one-dimensional heat kernel.)
- Consider the continuous piecewise linear function f(x) that is is
0 outside of [−2,2] and passes through the points (− 2,0),
(−1,2), (0,-1), (1,2), and (2,0). Find the Fourier transform of
f this way. First, find the distributional derivative f'', which is a
linear combination of δ functions. Then, find the FT
f''. Finally, use the FT to obtain the find Fourier transform of f.
- Use Laplace's method directly (don't simply apply the formula!)
and Watson's lemma to derive an asymptotic formula for the integral
$I(x) = \int_{-1}^1 (2+t^2)^{-x}dt$, $x\to \infty$.
Updated 4/24/2014 (fjn)
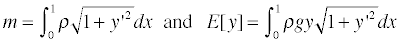 Assuming that the chain hangs in a shape that minimizes the
energy, find the shape of the hanging chain.
Assuming that the chain hangs in a shape that minimizes the
energy, find the shape of the hanging chain.