Math 642-600 Assignments — Spring 2018
Assignment 1 - Due Monday, 2/5/2018.
- Do the following problems.
- Problem 2, page 204 (§ 5.1).
- Problem 7, page 204 (§ 5.1).
- Hanging chain problem. A chain having uniform linear
density ρ hangs between the points (0,0) and (1,0). The total mass
m, which is fixed, and the total energy E of the chain are
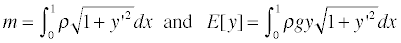 Assuming that the chain hangs in a shape that minimizes the
energy, find the shape of the hanging chain.
Assuming that the chain hangs in a shape that minimizes the
energy, find the shape of the hanging chain.
- Consider the functional J(y) =
∫abF(x,y,y′)dx, where y ∈
C1 and y(a)=A, y(b)=B are fixed.
- Let y extremize J, subject to all of the conditions above. Verify
that if η ∈ C1 and η(a)=η(b)=0,
then
Δ J = ∫ab (-g(x) +
Fy′(x,y,y′))η′(x)dx, where g(x) =
∫axFy(u,y,y′)du.
- Use (a) to show that -g+Fy′(x,y,y′)=c, a
constant. From this, it follows that
Fy′(x,y,y′)∈ C1. (Du
Bois-Reymond, 1879. The point is that one need not assume that
y′′ exists.)
- Smoothing spline. Let J[y] =
∫01 (y′(x))2dx. Let the
admissible set for J be all piecewise C1 curves on [0,1]
that satisfy y(k/n) = yk , for k = 0, 1, 2, ..., n, with
the discontinuities in y′ appearing only at the points
xk = k/n. Use
the previous problem to show that the minimizer for J is a linear
spline passing through all of the points {(xk,yk), k = 0,
..., n}. (Hint: y(x) is in C1[xk,
xk+1]).)
Assignment 2 - Due Monday, 2/12/2018.
- Do the following problems.
- Problem 5, page 204 (§ 5.1).
- Problem 9, page 204 (§ 5.1).
- Problem 11, page 204 (§ 5.1).
- Show that the functional $J(y):=\int_0^1( xy^2+y'^2)dx$ is
Fréchet differentiable, if the the $C^1[0,1]$ norm is used.
- The metric of a surface in $\mathbb R^3$ having parametric form
$x=x(u,v),y=y(u,v), z=z(u,v)$ is defined by $ds^2=E(u,v)du^2 +
2F(u,v)dudv +G(u,v)dv^2$. Consider the torus (surface of a
"doughnut") obtained by rotating a circle with center $(R,0,0)$ and
radius $r < R $ about the $z$ axis. Find the metric for it and use
it to obtain the 2nd order differential equations for the geodesics.
- Problem 6, page 205 (§ 5.2).
- Find the Legendre transformation H(p) for F(x) =
xT A x, where x is in
Rn and A is a symmetric, positive definite n×n
matrix.
Assignment 3 - Due Monday, 2/19/2018.
- Do the following problems.
- Suppose that the kinetic energy for a system is given by
$T(\underline{q}, \underline{q'})= \sum_{i,j=1}^n
A_{i,j}(\underline{q})q_i'q_j'$, where
$\underline{q}=(q_1,q_2,\ldots,q_n)$ and the matrix $A$ is positive
definite. (In matrix form, $T=\underline{q}'^{\,T}A\underline{q}'$.)
Use your solution to problem 7 in assignment 2 to find $T$ in terms of
$\underline{q}$ and $\underline{p}=(p_1,p_2,\ldots,p_n)$. Show that
the Hamiltonian has the form $H(\underline{q},\underline{p}) =
T(\underline{q},\underline{p}) +V(\underline{q})$.
- Problem 7, page 206 (§ 5.2). (See Fig. 5.4, p. 205 for a
diagram.)
- Problem 8, page 206 (§ 5.2). (Note: There is an error in the
expression for L. The (dθ/dt)2
sin2θ) should be replaced by
(dφ/dt)2 sin2θ.)
- For a planet having mass $m$ in orbit around the sun (mass=$M$),
the potential is $V(r)=-mMG/r$, where $G$ is the gravitational
constant. In addition, the polar form of its Lagrangian is $ L=m\dot
r^{2}/2 + mr^2 \dot \theta^{2}/2+ mMGr^{-1}$. ($\dot r=dr/dt$, and
$\dot \theta=d\theta/dt$).
- Show that the Hamiltonian $H=\frac{1}{2m}
(p_r^2+r^{-2}p_\theta^2) - mMGr^{-1}$.
- Show that the angular momentum $p_\theta=\ell$ is a constant of the
motion.
- Show that the Hamiltonian is a constant of the motion, $H=E$,
where $E$ is the total energy of the system. (To keep the planet in
a finite orbit, we need to have $E<0$.)
- Show that $p_r = \ell r^{-2} \frac{dr}{d\theta} = -
\ell \frac{d}{d\theta}(r^{-1})$.
- Let $u = r^{-1}- m^2MG\ell^{-2}$. Show that $2m E\ell^{-2} +
m^4M^2G^2\ell^{-4} = \big(\frac{du}{d\theta}\big)^2 + u^2$. To
simplify notation, let $\rho=(m^2MG\ell^{-2})^{-1}$ and
$\gamma=2m\rho^2 E \ell^{-2}$. This puts the equations above in the
form $u=r^{-1} -\rho^{-1}$ and
$\rho^{-2}(1+\gamma)=\big(\frac{du}{d\theta}\big)^2 + u^2$. (We assume
that $-1<\gamma<0$, so that $0< 1+\gamma <1$.) Solve this differential
equation for u in terms of $\theta$ and obtain $r=r(\theta)$.
- Use your solution to the previous part to establish Kepler's laws
of planetary motion:
- The orbit of a planet is an ellipse, with the sun at one
focus.
- The radius vector from the sun to the planet sweeps out equal
areas in equal times.
- The square of the period of any planet is proportional to the
cube of the semimajor axis of its orbit. The proportionality constant
is the same for all planets.
Assignment 4 - Due Monday, 2/26/2018.
- Read section 6.2.
- Do the following problems.
- Problem 4, page 205 (§ 5.2). (Attaching a mass at the
midpoint $x_c$ amounts to making changing the density from $\rho$ to
$\rho+ m\delta(x-x_c)$.)
- Problem 6, page 205 (§ 5.2). Find the Hamiltonian in terms
of $p=m\dot x$ and $q=x$. Find a first order ode that describes the
system. (Hint: use conservation of energy.)
- Problem 1, page 207 (§ 5.4). (Hint: Use Minimax Principle.)
- Use a quadratic polynomial to estimate the lowest eigenvalue for
the Sturm-Liouville problem with Lu = − u′′ =
λu, u(0) = 0, u′(1)+u(1) = 0.
- Problem 6, page 208 (§ 5.4). Take Ω to be a 2D disk
centered at 0 and having radius r = a. How does the lowest
eigenvalue change with a? Explain.
Assignment 5 - Due Wednesday, 3/7/2018.
- Read sections 6.2 and 6.4.
- Do the following problems.
- Do problems 4, 5, 11, 12, 15 in
the
Exercises for Complex Variables
- Section 6.1: 4, 6
- Section 6.2: 6, 9, 10, 11
- Section 6.4: 1
- Find all of the Laurent expansions about $z=0$ for $f(z) =
\frac{1}{(z^2-1)(z+2)}$.
- Let $C_0$ and $C_1$ be simple closed curves, with $C_0$ contained
in the interior of $C_1$. Suppose that $f(z)$ is analytic on the two
curves and in the region between them, and that there is a simple
closed curve $C$ in the region between $C_0$ and $C_1$. Show that all
of the coefficients of the Laurent expansion for $f$ are given by
$a_n=\frac{1}{2\pi i}\int_{C} \frac{f(\zeta)}{(\zeta -
z)^{n+1}}d\zeta$.
- (Isolation of zeros.) Suppose that $f(z)$ is analytic in the disk
$|z-z_0| < R$ and that $f(z_0)=0$. Show that if $f(z)$ is not
identically 0, then there exists $0<\rho< R$ such that $f(z)\ne 0$ for
all $z$ in $0<|z-z_0| \le\rho$. Use this to show that
$\sin^2(z)+\cos^2(z) = 1$ for all $z\in \mathbb C$, given that it holds
for all real $z$.
Assignment 6 - Due Wednesday, 3/21/2018.
- Read section 6.5.1, 6.5.2 and 7.1.
- Do the following problems.
- Section 6.4: 3, 7 (assume $a$ and $k$ are positive), 9, 20, 25.
- Suppose that $f(z)$ has a pole of order $m>1$ at $z=z_)$. Show
that $\mathrm{Res}_{z_0}f=
\frac{1}{(m-1)!}\frac{d^{m-1}}{z^{m-1}}\big\{(z-z_0)^mf\big\}(z_0)$. Use
this to find the integral $\int_{-\infty}^\infty \frac{e^{i\omega
x}}{(1+x^2)^2}dx$.
- Suppose that $f(z)$ is analytic in and on a positively oriented
simple closed curve $C$, except for isolated singularities at
$z_1,z_2,\ldots,z_n$ inside the curve, and one simple pole at a
point $z_0$ on the boundary. If $z_0$ is at a corner of the curve
and if the exterior angle at the corner is $\alpha$, show that, in
the sense of principal values,
\[ \oint_Cf(z)dz= 2\pi i\sum_{j=1}^n \mathrm{Res}_{z_j}(f) + i\alpha
\,\mathrm{Res_{z_0}}(f). \]
- Let $\xi \in \mathbb R$ and consider the integral
$G(\xi)=\int_{-\infty}^\infty e^{-x^2}e^{i\xi x}dx$. Show that
$G(\xi)= \sqrt{\pi}e^{-\xi^2/4}$, given that $G(0)=\sqrt{\pi}$.
- The Gamma function has simple poles at $z=�0,-1, -2,
\ldots$. Show that the residue at $z=-n$ is
$\frac{(-1)^n}{n!}$. (Hint: use $\Gamma(z+1) = z\Gamma(z)$.)
Assignment 7 - Due Wednesday, 4/11/2018.
- Read section 7.2.1.
- Do the following problems.
- Section 6.5: 3(a), 7, 8(b), 9 (Just do $J_{3/2}$.), 13, 22
- Show that the Wronskian
$W(J_{-\nu}(z),J_\nu(z))=\frac{2\sin(\pi \nu)}{z}$.
- Section 7.1: 1
Assignment 8 - Due Wednesday, 4/25/2018.
- Read section 7.2.1 and 7.2.3.
- Do the following problems.
- Let $L$ be a bounded linear operator on $\mathcal H$; that is, $L
\in {\mathcal B}(\mathcal H)$. Show that $\rho(L)$ contains the
exterior of the disk $\{\lambda \in {\mathbb C} \colon |\lambda|
\le ||L||\}$. (Consequently, $\sigma(L)$ is contained in the disk.)
- Section 7.1: 2(a), 2(b). For each operator in 2(a), 2(b), find
the norm and adjoint $L^\ast$. (You may use problem 1 above.)
- Let $L = L^\ast$ be defined on a domain $D$. In class, we showed
that $\sigma_r(L) = \emptyset$ and that $\sigma_d(L) \subset \mathbb
R$. Show that $\sigma_c(L) \subseteq \mathbb R$. Thus, $\sigma(L)$
is a subset of the reals.
- Let $L=A$ be a self-adjoint, $n\times n$ matrix. Suppose that $A$
has $r$ distinct eigenvalues, arranged in the order $\lambda_1 <
\lambda_2 < \cdots < \lambda_r$. In addition, let the orthogonal
projections onto the eigenspaces be $Q_1,\ldots,Q_r$. Suppose $a <
b$, and neither is an eigenvalue of $A$; let $C_\varepsilon$ be a
positively oriented rectangular contour, with corners
$a-i\varepsilon$, $b-i\varepsilon$, $b+i\varepsilon$, and
$a+i\varepsilon$. Show that \[ \lim_{\varepsilon\downarrow
0}\,-\frac{1}{2\pi i} \oint_{C_\varepsilon} (A-\lambda I)^{-1}d\lambda
= E_b-E_a, \] where $E_\lambda := \sum_{j=1}^r H(\lambda - \lambda_j)Q_j$
and $H(t)=\begin{cases} 1 & t\ge 0\\0 & t<0\end{cases}$.
- Find the Green's function for the operator $Lu = -u''$, with
$D_L=\{u,u''\in L^2[0,\infty): u'(0)=0\}$. Use it and Stone's formula for the
spectral family of $L$ to derive the Fourier cosine transform pair:
\[
F(\xi)= \frac{2}{\pi}\int_0^\infty f(x)\cos(\xi x)dx \ \text{and}\
f(x)= \int_{0}^\infty F(\xi)\cos(\xi x)d\xi
\]
Assignment 9 - Not to be handed in.
- Suggested problems (Fourier transform convention: $\hat f(\xi) =
\int_{-\infty}^\infty f(x)e^{-i\xi x}dx$.)
- Prove the following theorems:
-
If $f,g \in L^1(\mathbb R) \cap L^2(\mathbb R)$, then $f\ast g\in
L^1(\mathbb R) \cap L^\infty(\mathbb R)$.
- Section 7.2: 6(a,b,c).
- Consider the one dimensional heat equation, $u_t = u_{xx}$, with
$u(x,0) = f(x)$, where $-\infty < x < \infty$ and $0 < t <
\infty$. In 7.2.6(c) you found that, after scaling, ${\mathcal
F}[e^{-x^2}] =\sqrt{\pi}e^{-\xi^2/4}$. By taking the Fourier
transform in $x$, show that the solution $u(x,t)$ is given by
\[
u(x,t) = \int_{\mathbb R}K(x-y,t)f(y)dy,\ K(\xi,t) =
(4\pi t)^{-1/2} e^{-\xi^2/4t}.
\]
(The function $K(\xi,t)$ is the one-dimensional heat kernel.)
- Let T be a tempered distribution. Find the Fourier transforms for
T′, xT(x), T(x−a), and eibxT(x).
- Let $f$ be in Schwartz space, $\mathcal S$, and let $g$ be
$C^\infty$ and satisfy $|g^{(m)}(x)| \le c_m(1+x^2)^{n_m}$ for all
nonnegative integers m. Here $c_m$ and $n_m$ depend on $g$ and
$m$. Show that $fg$ is in Schwartz space. Use this result to explain
how to define the product $g(x)T(x)$, where $T$ is a tempered
distribution.
Updated 4/27/2018 (fjn)
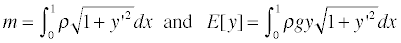 Assuming that the chain hangs in a shape that minimizes the
energy, find the shape of the hanging chain.
Assuming that the chain hangs in a shape that minimizes the
energy, find the shape of the hanging chain.