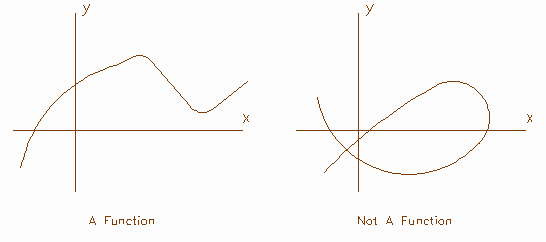(c) copyright Foundation Coalition (S. A. Fulling) 1997
Classes 1.2, 2.1, 2.M
Functions
Reading assignment for Friday, September 5
- Calclabs 2.1, 2.2, 14.2
- The material on this Web page about exponentials and logarithms
- Recommended: Stewart pp. 17-21 (in 0.2),
Appendix A (emphasis on the absolute value function),
Appendix B (emphasis on equations of lines),
0.3
Reading assignment for Wednesday, September 10
- This Web page
- Stewart 0.1
Reading assignment for Thursday, September 11
- Stewart pp. 21-25 (in 0.2)
- Instructions for "Shifting and Scaling" drill
- Recommended:
Stewart Appendix D (emphasis on graphs of the sine and cosine functions),
Appendix C
On Friday (class 1.2) we continue exploring Maple,
with emphasis on the distinction
between "functions" and "expressions" in Maple syntax.
At the same time we'll review some mathematical functions that are (for
the most part) already familiar to you, before discussing exactly what the
word "function" means.
These include the absolute value function, linear functions, power functions,
sine and cosine, exponentials, and logarithms.
They provide the raw material for all the examples and problems in the rest of
calculus.
Also, some of them will be put to work in your engineering course this week.
On the following Wednesday (class 2.1)
we make a deeper analysis of the function concept.
Exponential and logarithmic functions
In the list of elementary functions, the ones that you are least likely to
have studied in depth in high school are the exponentials and logarithms.
Stewart also has very little to say about them at this stage.
Some understanding of them is necessary, however, for your work in engineering
class on graphing of quantitative relationships.
We will study these functions in detail next semester
(see Stewart, Chapter 6).
Today we just mention a few basic facts about them and help you get
acquainted with their qualitative behavior (what their graphs look like).
[READ US!]
Functions in applications
So far we have thought of a function as represented by a formula, such as
y = 3x + 2.
The main point of class 2.1 is that
a function is not the same thing as a formula, and in fact most functions
do not have formulas corresponding to them.
In order to search for a proper definition of "function",
let's contemplate some examples of the functions that arise in engineering and
other subjects that apply calculus.
- The position of a falling body, as a function of time.
You may know from high-school science, and will certainly hear in physics
class very soon, that when an object is dropped from rest, the distance
it travels is
x = 1/2 g t2
as a function of time. In this case the function is indeed given by a
formula.
- The temperature in our classroom, as a function of time.
At any time t, we can read a thermometer in the room and get a
number; we can plot these numbers on a graph.
If the thermostat doesn't work very well, the numbers will not be constant,
and the graph will be some random curve.
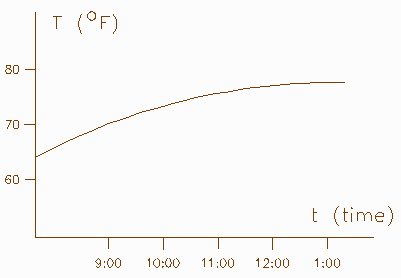
This is the graph of a temperature function,
T = g(t).
Ordinarily we would not expect to have an exact algebraic formula
for this function; it is simply empirical data.
(In fact, in practice the situation is usually even worse than this:
The temperature will be measured only at some finite set of times,
and there will be some error
(meaning unavoidable experimental inaccuracy, not a human blunder)
in each data point.
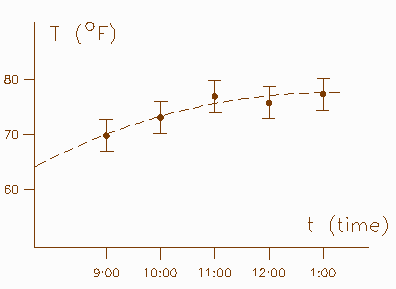
We idealize the situation and have faith that there is some
well-defined "true" temperature function to which the thermometer readings are
an approximation. However shaky this stance may be philosophically,
it is a tremendously powerful point of view for describing and partially
controlling the world we live in, through science and engineering.)
If we are very lucky (for instance, if we do have a good thermostat),
we may be able to come up with a theoretical formula that predicts the
temperature g(t) well, such as
T = 75 - 5 exp (-t/10).
For practice,
- sketch this function;
- discuss the units of the 3 numerical constants in it.
- The interest rate paid by a bank, as a function of time (date).
Usually a bank will not change its rate more often than once a day,
so the graph of this function is really just a string of points, one for each
day.
We could think of the interest as a piecewise-constant function
of time measured in seconds
(similar to the cost of mailing a letter or making a long-distance
telephone call -- see Stewart, Example 15, pp. 9-10).
On a longer time scale, however, it is possible to idealize
the situation by filling in a smooth curve through the points.
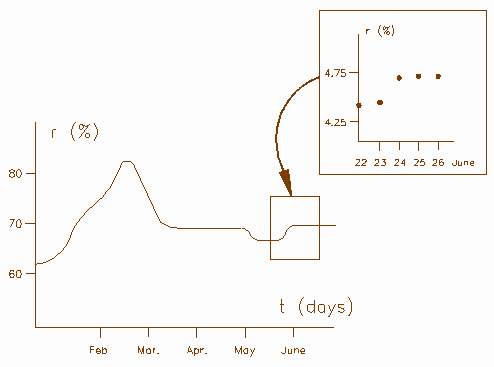
Economists can now do calculus with this function, pretending
that the interest rate varies continuously with time like the temperature in
the room.
It is useful to deal with interest rates in this way,
even though in this case the smooth curve through the data points is not just
philosophically shaky, but downright fictitious!
These examples show that, in "real life", a function is most likely to be
encountered as either
- a list of numbers, or
- a graph,
rather than a formula.
Either of these kinds of concrete experiences forms the basis for an abstract
definition of the term "function".
So, what is a function?
Let us look at some ways that various people have tried to answer this
question.
- Stewart's textbook says:
A function f is a rule that assigns to each element x
in a set A exactly one element, called f(x), in a set
B.
This definition can be criticized because the word "rule" suggests a
formula, and we agreed that a formula is not necessary to have a function.
- Vaguer words have been used:
A function is an assignment of a number, y, to each number,
x, in some set of numbers, called the domain of the function.
It is fair to ask, "But then what is the definition of 'assignment'?"
- Once a class was asked on a test to define "function".
One student wrote:
A function is when every x value is assigned to only one
y value.
That "is when" would not get past a grader in an English composition class.
But the sentence does express the essential point.
What all these definitions are trying to say is that a function is some
kind of imaginary machine that processes each number x (the
input) into a number y = f(x) (the output).
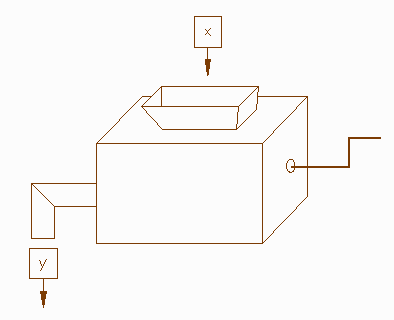 This is our primary notion of function.
This is our primary notion of function.
- On the other hand, another calculus book says:
A function with domain A is a set W of ordered pairs such
that for each x in A, there is exactly one ordered pair
(x,y) in W having x in the first position.
What on earth does all that mean? Although this definition of a function
is quite common in books on pure mathematics, we believe that beginning
students are better off thinking of functions in the "machine" sense.
However, this definition does have a concrete counterpart that deserves
emphasis:
- We have seen that a function can be given to us by a graph.
However, not every curve is the graph of a function.
Vertical line test: A curve in the x-y plane is the
graph of a function of x if and only if no vertical line
intersects the curve more than once.
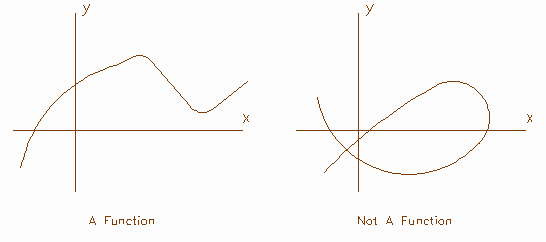 The "ordered pair" definition says, in effect, that a function is the same
thing as a graph of a function.
The graph, as an abstract mathematical object, is the function.
(Or, if you prefer, the graph (as an actual drawing on paper)
is a picture of the function.)
The "ordered pair" definition says, in effect, that a function is the same
thing as a graph of a function.
The graph, as an abstract mathematical object, is the function.
(Or, if you prefer, the graph (as an actual drawing on paper)
is a picture of the function.)
In summary, there are two equivalent concepts of "function":
- An abstract machine for processing numbers (or other entities).
- A graph that passes the vertical line test.
A function is such a fundamental concept of mathematics that it is not
surprising that we have trouble giving a crisp definition of it in terms of
more elementary concepts.
Instead, we form an intuitive concept of function and later define
other mathematical words in terms of it.
Be prepared for class exercises on
- domains and ranges of functions
- composition of functions