(c) copyright Foundation Coalition (S. A. Fulling) 1997

Class 6.3 (and 17.M)

Polar Coordinates and Polar Unit Vectors

Reading assignment for Friday, October 10

Stewart 9.4 (Skip "Tangents to polar curves," pp. 569-570.)
This Web page
Take a peek ahead into Chapter XII of Don't Panic to see how polar unit vectors will be used.

Like all of this week, today is an insertion into the standard syllabus of first-semester calculus to provide some tools needed by physics to describe a world of more than one dimension. The first topic, polar coordinates, is traditionally treated somewhere later in the calculus sequence. The second topic, polar unit vectors, doesn't appear at all in most calculus textbooks. Nevertheless, this is the logical place for us to introduce it in both math and physics classes. We will come back to it next semester in physics class and a math lab.

Polar coordinates

The gravitational force of the earth on a satellite depends primarily on the distance of the satellite from the center of the earth. This is an example of a wide class of problems in which the most important property of a point in space is its distance from some special point. A sensible first step is to choose the special point as the origin of the coordinate system. But, often it is useful to go further: Instead of specifying the variable point by its x and y coordinates relative to some arbitrary choice of axes through the origin, why not label the point by the most pertinent quantity, its distance from the origin, together with some indication of its direction from the origin? In two-dimensional space, the direction can be specified by a single number, the angle between the vector to the point and some axis.

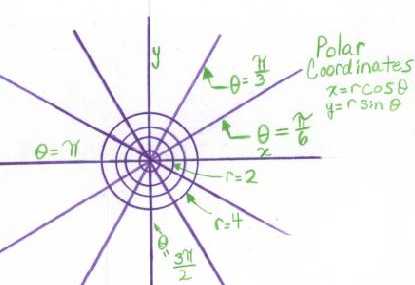
In this way we arrive at the polar coordinate system in the plane. By definition, r is the distance of our variable point from the origin, and Ð is the angle between the positive x axis and the vector representing the point.

Note: Since the Web does not yet speak Greek easily, we will use the Icelandic letter Ð for "theta".

The formulas expressing the Cartesian coordinates of the point in terms of the polar coordinates are (by elementary trigonometry)

x = r cos Ð, y = r sin Ð. (1)

Going back the other way is slightly more complicated. Finding r is easy: Squaring both of equations (1) and adding and taking the square root (or just remembering the formula for the distance between two points) you find

r = (x² + y²)^1/2. (2)

But finding Ð raises some technicalities. Dividing the second of equations (1) by the first, we get

tan Ð = y/x. (3)

If you already know about the inverse tangent function (Stewart Sec. 6.6), you may be tempted to write

Ð = arctan y/x = tan^-1 y/x,

but this is not quite correct. Read more about the technicalities of defining theta. (not yet available)

Polar unit vectors

Let's return to the problem of a satellite orbiting the earth, and consider a vector v = < v_x, v_y> associated with the satellite, such as the velocity or acceleration of the satellite. (Recall that it is best to represent such a vector by an arrow with its tail at the position of the satellite, which serves as the origin of the satellite's private coordinate system.) For analyzing the physics in the earth's gravitational field, the most useful decomposition of v is not into its Cartesian components v_x and v_y, but rather into its component in the direction to (or from) the earth and its component in a direction perpendicular to that one. From that point of view the physics is simple -- almost one-dimensional!

In other words, we want to replace the satellite's private Cartesian coordinate system by a rotated coordinate system. This is the same as the orthogonal basis problems we looked at on day 6.1, with the added complication that the new orthogonal basis now varies from point to point in space. At each point, we need to find a pair of orthogonal unit vectors, one pointing in the radial direction and the other in the direction of increasing theta; and then we need to practice decomposing an arbitrary vector into components along those two basis vectors.

It is important to distinguish this calculation from another one that also involves polar coordinates. Given a vector v = < v_x, v_y>, we could represent it by its polar coordinates, using formulas like (1)-(3) above, but with v_x and v_y in place of x and y. (Then the analogue of r would be the speed of the satellite, if v is the velocity.) That is sometimes a very useful thing to do, but it is not what we are talking about now.

Here is a picture of what we are talking about now, for the case where the point r = (x,y) is in the first quadrant. The formulas we derive from it will actually be correct in all four quadrants, as you can check.

[insert drawing] (not yet available)

Let the point r have polar coordinates (r,Ð) (related to (x,y) by equations (1)-(3)). We want i_r to be a unit vector at r pointing in the direction of increasing r, and i_Ð to be a unit vector at r pointing in the direction of increasing Ð. We specify these vectors, as usual, by listing their ordinary Cartesian components; that is, finding equations of the form i_r = < a₁, a₂> = a₁i + a₂j. However, the components a₁ and a₂ will be functions of r and Ð, because what is meant by "the direction of increasing r," etc., varies from point to point!

Method 1: We can find these polar unit vectors by geometric and trigonometric reasoning.

We already know a vector that points in the direction of increasing r, namely, the vector r = < x,y> itself. To form a unit vector, we need only to divide this vector by its length:
i_r = r/r = < cos Ð, sin Ð>. (4)
To find a vector perpendicular to a given one in dimension 2, you just interchange the components and change one of the signs. (This is the vectorial version of the elementary prescription, "The slope of the perpendicular line is the negative of the reciprocal of the slope of the original line.") Thus
i_Ð = < - sin Ð, cos Ð> (5)
or its negative. It is clear from the drawing that (5) is the vector with the correct overall sign.

Method 2: Here is a more systematic approach, using the concept of tangent vector.

x = r cos Ð, y = r sin Ð,

with Ð regarded as a constant. Thus the tangent vector is

< dx/dr, dy/dr> = < cos Ð, sin Ð>.

This is already a unit vector, so it is the desired i_r. This reproduces the result (4).

Similarly, to move in the direction of increasing Ð means to move along a curve on which r is constant and Ð is increasing. (This is a circle centered at the origin.) The parametric equations are still equations (1), but now Ð is the variable and r is the constant. Thus the tangent vector is
< dx/dÐ, dy/dÐ> = < - r sin Ð, r cos Ð>.
This is not a unit vector: it has length r. (This is not surprising geometrically, if we think of the tangent vector as the velocity, with Ð as time. If r is greater than 1, then a little change in Ð goes a long way; the moving point must move fast in order to get all around the circle in time 2*Pi. If r is smaller than 1, a given change in Ð produces only a small movement of the point, dwindling to no motion at all when r = 0.) Dividing by the length produces the unit vector i_Ð found in (5).

Challenge problem: Define coordinates u and v by

x = (u² - v²)/2, y = uv.

Use Method 2 to find formulas for the pair of perpendicular unit vectors i_u and i_v that point in the directions of increasing u and increasing v, respectively.
Sketch these unit vectors at the point where u = 2 and v = 1. Also sketch the curve through that point along which v is constant, and the one along which u is constant. Hint: These are called parabolic coordinates.

Now that we have the polar unit vectors, we can express other vectors in terms of them. Let us consider the constant vector

E = < 3, -1> = 3i - j.

Since i_r is a unit vector, the vector projection of E onto i_r is

(E.i_r)i_r = (3 cos Ð - sin Ð)i_r.

Similarly, the component of E along i_Ð is

- (3 sin Ð + cos Ð) i_Ð.

Since the polar unit vectors are an orthogonal basis, the sum of these two vectors is the decomposition of E into its components in the radial and angular directions (which is the goal of our calculation in this example):

E = (3 cos Ð - sin Ð)i_r - (3 sin Ð + cos Ð) i_Ð.

By substituting the formulas (4) and (5) for the polar unit vectors into this equation and simplifying, you can verify that the equation is correct.

Although E is a constant vector (not a function of the point r), its decomposition does depend on the coordinates of the point. Actually, we notice that it depends on Ð but not on r. Can you explain that geometrically?