Teaching
Research
Publications
Talks
Main
Picture Gallery
A picture from the paper on amenable groups. It is a piece of an orbit of a three-generated non-elementary amenable group, based on the Penrose tiling.
Left picture is a Schreier graph of the action of IMG(z^2+i) drawn in a way coming from a continuous surjection of the Julia set of z^2+i onto the triangle. There is an uncountable family of similar surjections of dendrites onto the triangle. Each dendrite is a z-slice of the Julia set of the 2-dimensional map F(z, p)=((1-2z/p)^2, (1-2/p)^2). One of these surjections (corresponding to p=0, 1, or \infty) is the well known Sierpinski plane filling curve, shown on the right hand side. For more details, see my preprint.
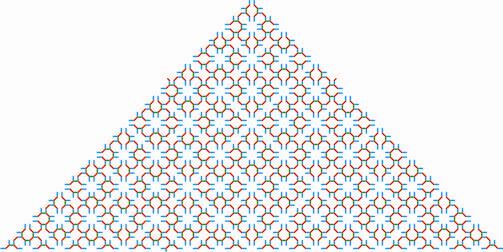
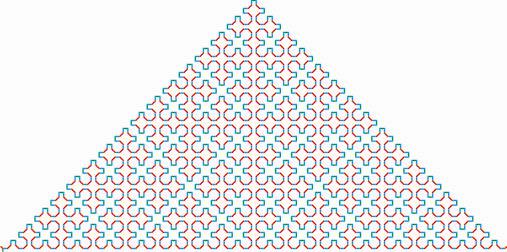
Schreier graphs of groups belonging to a self-similar Cantor set of groups (see a preprint and a paper).

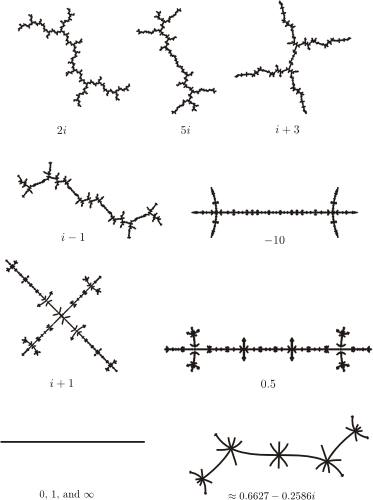
Slices of the Julia set of F(z, p)=((1-2z/p)^2, (1-2/p)^2). The corresponding value of p is written under the dendrites. The dendrite corresponding to p=2i is affine conjugate to the Julia set of z^2+i. The function and the corresponding Julia set is studied in my preprint.
Schreier graph of IMG(z^2+i) again, drawn to fill the "tame twin dragon" via mating with itself. See details in the last section of my book. Figure 6.26 in the book illustrates the same phenomenon, but the picture below is probably a bit more elegant.

Another version illustrating the mating of z^2+i with itself. This time it shows the loop going around the dedrite:
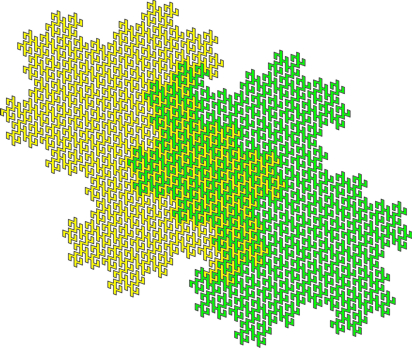
Yet another way to draw the Schreier graphs of IMG(z^2+i), this time coming from mating z^2+i with z^2+c for c equal to the landing point of the external ray an the angle 5/14.


Some examples from the uncountable family of Julia sets described in my preprint.
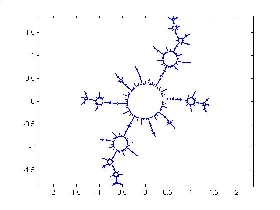
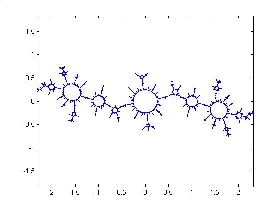
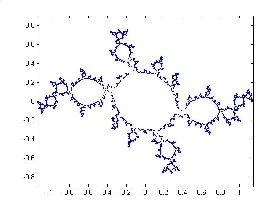
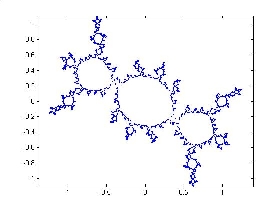
Below are more of such Julia sets together with their position in the parameter space. See movies on the web page of Laurent Bartholdi showing sequences of these Julia sets as the parameter changes continuously. Collection of nice movies describing related (though different) phenomena can be found on the web pages of Arnaud Chéritat and Sarah Koch.
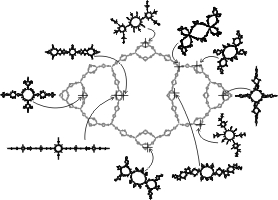
The Schreier graph of the iterated monodromy group of the polynomial z^2-0.2282..+1.1151..i obtained from the paper-folding procedure. See my preprint.

The limit of the above Schreier graphs is a continuous surjection of the Julia set of the polynomial onto the sphere also coming from a mating, as described in a paper of J.Milnor.
One can also construct an uncountable family of surjections from the dendroids, which are z-slices of the Julia set of the map F(z, p)=((1-2z/(p+1))^2, ((1-p)/(1+p))^2) onto the sphere. Approximation of these surjections can be also constructed using the paper-folding procedure. Pictures below show two different Schreier graphs. The one on the left is a deeper version of the previous roundish Schreier graph. The corresponding dendroids are shown on the picture below.

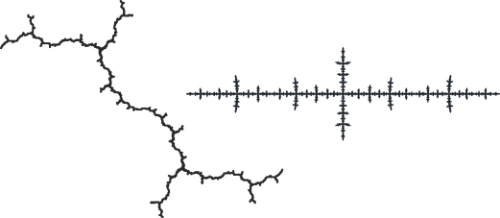
Limit space of a group generated by the three-state automaton over a two-letter alphabet (a=\sigma(a, a), b=(c, b), c=(a, a)).
All three pictures describe the same space. The first picture is the upper half of the Julia set of (1-z)^2/(1+z)^2 after a conformal transformation.



Limit space of another group generated by the three-state automaton (a=\sigma(b, b), b=(b,c), c=(b, a)). It is the upper half of the Julia set of 1-1/z^2.
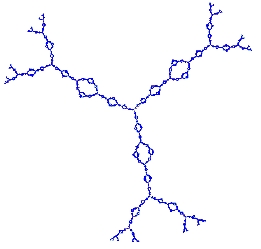
Limit space of a torsion group described by Said Sidki in his paper "Automorphisms of one-rooted trees: growth, circuit structure and acyclicity", J. of Mathematical Sciences (New York), 100, no 1, (2000), p. 1925-1943. It is generated by a=\sigma, b=(a, a), c=(b, 1), d=(c, d).
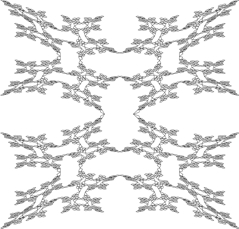
The Schreier graph of the action of the iterated monodromy group of the ``airplane'' polynomial on the 10th level of the binary tree. Each color corresponds to a generator, which act by the recurrent rule a=\sigma(1, c), b=(1, a), c=(b, 1).
