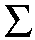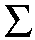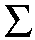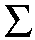Next: 2.iii. Real Solutions to Sparse Polynomial
Systems
Up: 2.ii. Polyhedral Homotopy Algorithm: Table
of Contents
Previous: 2.ii.b. Regular Triangulations
2.ii.c. Polyhedral homotopy algorithm
Crucial to the polyhedral homotopy algorithm of Huber and
Sturmfels [HS] are polynomial
systems derived from the original system and the regular subdivision
Pw of
P by a lifting function w.
Given a polynomial f with Newton polytope P and a face
F of the subdivision Pw, consider the sum of terms of
f with exponent vector in the face F, restricting f
to the face F.
Doing this for each polynomial fi in our original system, we
obtain the facial subsystem of (2.1)
given by F.
Suppose we have a lifting function
w : Lattice Points in P --> Q
and a polynomial f with Newton polytope P
| f(x) =
| 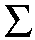 |
ca xa , |
the sum over all integral lattice points a in P.
We multiply the term with exponent a by
tw(a) to obtain
| f(x;t) :=
| 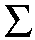 |
ca xa
tw(a) ,
|
the sum over all integral lattice points a in P.
Modifying all polynomials in the original sparse system in this way gives
the lifted system, a family of sparse systems depending upon the
parameter t.
|
f1(x;t) =
f2(x;t) =
... = fn(x;t)
= 0 , |
(2.4) |
Solutions to this system are algebraic functions
t |--> x(t) in the
parameter t.
In a neighborhood of 0 in the complex plane, each branch is expressed as a
Puiseaux series
x(t) =
(x1(t), x2(t), ...,
xn(t)) with
xi(t) =
tui yi +
higher order terms in t ,
where the yi are non-zero constants and exponents
ui are rational numbers.
Substituting this expression into (2.4), we obtain
| 0 = |
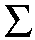 |
ca ya
tua + w(a)
+ higher order terms in t .
|
(The sum here is once again over all integral lattice points a in
P.)
The exponent of t is the dot product of
(u,1) with (a,w(a)).
Thus the terms of lowest order in t correspond to points
(a,w(a)) in the lifted polytope where the exponent vector
(u,1) achieves its minimum--a
face in the lower hull of the lifted polytope.
Let F be the corresponding face of the regular subdivision
Pw.
Let b be any vertex of this face F.
Removing the common factor
tub + w(b) from these lowest
order terms gives the restriction of f to the face F.
Thus the coefficients yi of the leading terms of the
Puiseaux expansion are solutions to the facial subsystem of the original
system (2.1) given by the face F
selected by the initial Puiseaux exponents.
Suppose the original system is general in the sense that each of its facial
subsystems given by faces F of the regular subdivision has solutions
only if VolF>0, that is, only if F is a facet of the subdivision.
Consider substituting the Puiseaux series into the polynomial
system (2.4) and then taking the limit
as t approaches 0.
The resulting polynomial system for the leading coefficients y of the
Puiseaux series are solutions to the corresponding facial system.
By previous assumption, this has no solutions unless F is a facet of
the subdivision Pw.
In that case, the inward pointing normal vector (u,1) to the
corresponding facet of the lifted polytope gives the initial exponent u
of the Puiseaux expansion.
The full Puiseaux series can be reconstructed from its initial terms
(see [HS] for details) giving the
1-1 correspondence
|
Solutions to facial subsystems of (2.1)
given by facets of Pw |
<----> |
Branches of the algebraic
function t |--> x(t) near t=0
|
This is the number of solutions to the lifted
system (2.4) for general complex numbers
t, so the number of solutions to the original sparse
system (2.1) equals the
number of solutions to all the facial subsystems given by facets of
Pw.
Now suppose the regular subdivision Pw is a regular
triangulation and each facial subsystem is general.
Then the facets F of Pw are simplices with no
interior vertices.
Since general sparse systems whose Newton polytope is such
a simplex have exactly n!Vol(F) solutions, the number of
solutions to facial subsystems given by facets of Pw
is exactly the sum of the normalized volumes of all facets of
Pw, which is
the normalized volume of P.



Next: 2.iii. Real Solutions to Sparse Polynomial
Systems
Up: 2.ii. Polyhedral Homotopy Algorithm: Table
of Contents
Previous: 2.ii.b. Regular Triangulations