| g(t) := (1, t, t2/2, ..., tn-1/(n-1)!) = | 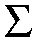 |
ti-1ei /(i-1)! , |


The results of
Section 4 were
inspired by a remarkable conjecture of Boris Shapiro and Michael Shapiro.
Let g : R --> Rn
be the rational normal curve
| g(t) := (1, t, t2/2, ..., tn-1/(n-1)!) = | 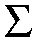 |
ti-1ei /(i-1)! , |
| linear span of g(t), g'(t), ..., g(i-1) | (5.1) | |
| Row space of the i by n matrix whose (j,l)-entry is tl-j/(l-j)! | (5.2) | |
| The i-plane osculating the rational normal curve g at g(t). | (5.3) |
| Ya1 F.(t1), Ya2 F.(t2), ..., Yas F.(ts), | (5.4) |
Eisenbud's and Harris's dimensional transversality result [EH, Theorem 2.3] guarantees that the intersection (5.4) is zero-dimensional. Not only does Conjecture 5.1 state that the classical Schubert calculus is fully real, but it also proposes flags witnessing this full reality. This conjecture has been central to subsequent developments in the real Schubert calculus and it has direct connections to other parts of mathematics, including linear systems theory and linear series on P1 (see Remark 5.8). The article [So7] and the web page [So4] give a more complete discussion.
One aspect of this conjecture which we relate is the following.
Consider these osculating flags F.(t) in more detail.
If the ith row of the matrix (5.2)
is multiplied by ti (which does not affect its row space
when t is non zero), then the entry in position (i,j)
is tj/(j-i)!, and so we have
| (5.5) |
| Ya F.(t1), Ya F.(t2), ..., Ya F.(t(n-k), | (5.6) |
This establishes a weak form of Conjecture 5.1 for simple Schubert conditions, replacing the quantifier for all ti in R by there exists ti in R.
If the parameters ti in (5.6) vary, then the number of real points in that intersection could change, but only if two points first collide (prior to spawning a complex conjugate pair of solutions). This is the reverse of the progression in Dietmaier's algorithm, as displayed in Figure 6. This situation cannot occur if the intersection remains transverse. Together with Theorems 5.2 and 5.3 we deduce the following result.
If t > 0, then by (5.5) the Plücker
coordinates of Fi (t) are strictly positive.
An upper triangular n by n-matrix g
is totally positive if every i by i subdeterminant of
g is non-negative, and vanishes only if that
subdeterminant vanishes on all upper triangular matrices.
For example, when t > 0 and i=n, the
matrix (5.2) is totally
positive.
Write G(t) for this matrix.
It has the form exp(th) where h is the principal nilpotent
matrix G'(t).
Observe that if t1 < t2 < ... <
ts, then
There is some experimental evidence for this version of Conjecture 5.1. Subsequent conjectures involving osculating flags have versions involving totally positive matrices. We leave their statements to the reader, they will be explored more fully in [So11].

