
|

|
|
|
Last modified: Mon May 15 20:27:49 EDT 2017
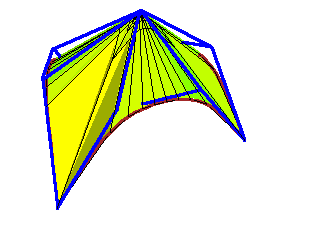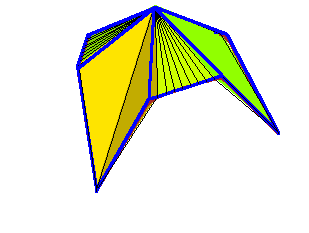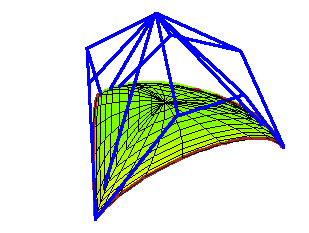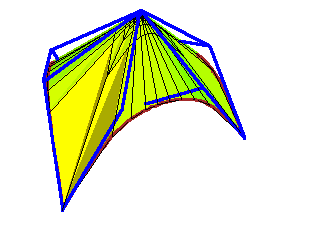
The control polygon of a Bézier curve is well-defined and meaningful---there is a sequence of weights under which the limiting position of the curve is the control polygon. For a Bézier surface patch, there are many possible polyhedral control structures, and none are canonical. We propose a not necessarily polyhedral control structure for surface patches, regular control surfaces, which are certain C0 spline surfaces. While not unique, regular control surfaces are exactly the possible limiting positions of a Bézier patch when the weights are allowed to vary, but the control points are fixed.
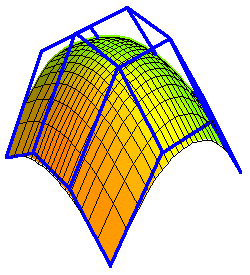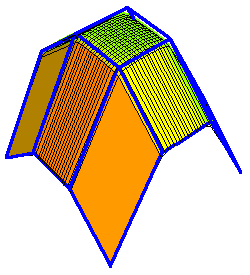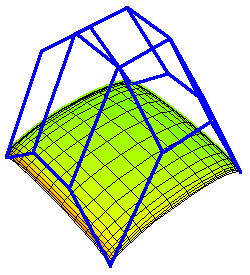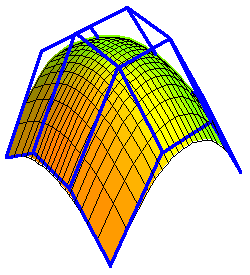
Below are some animations of toric degenerations.
The first are tensor product patches of bidegree (4,3) degenerating
into a union of triangular and bilinear patches in which not all
control points participate. (The second has limits at t → 0 and
t → ∞.) These are linked to larger animations.
The third shows a cubic Bézier triangle degenerating into nine triangles, and
the fourth a bicubic batch degenerating into nine bilinear patches, which happen to
be planar quadrilaterals.




Last modified: Mon May 15 20:27:49 EDT 2017