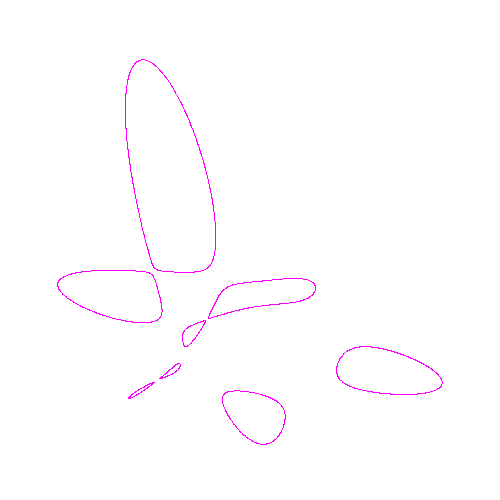|
Hessian of quartic with 4 ovals
|

|
|
|
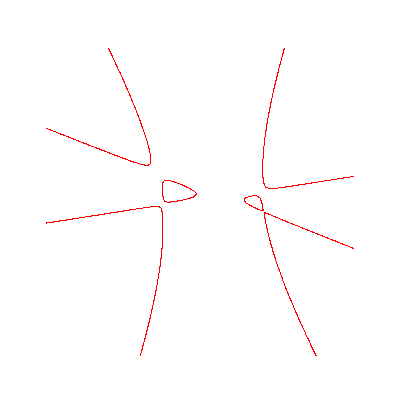
Hessian of quartic with 2 ovals
and 4 unbounded components
|
|
|
|
|
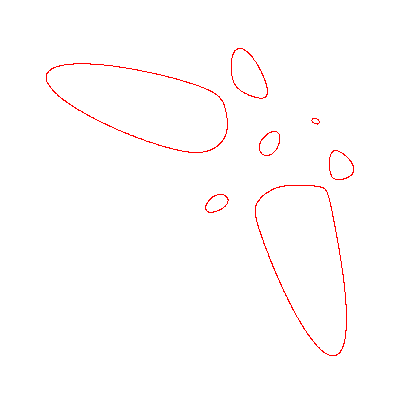
Hessian of quintic with 7 ovals
|
|
|
|
Another Hessian of a quintic with 7 ovals
|

|
|
|
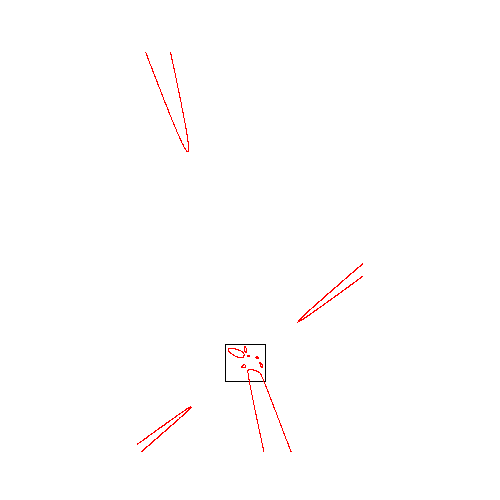
Hessian of quintic with 6 ovals
and 4 unbounded components
|
|
|
Hessian of quintic with 6 ovals
and 4 unbounded components
(close up)
|
|
|
|
|
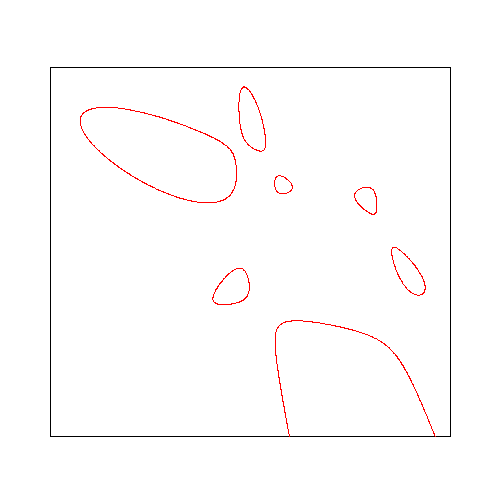
Hessian of quintic with 7 ovals and 2 unbounded components
|

|
|
|
|
Hessian of quintic with 8 ovals
|
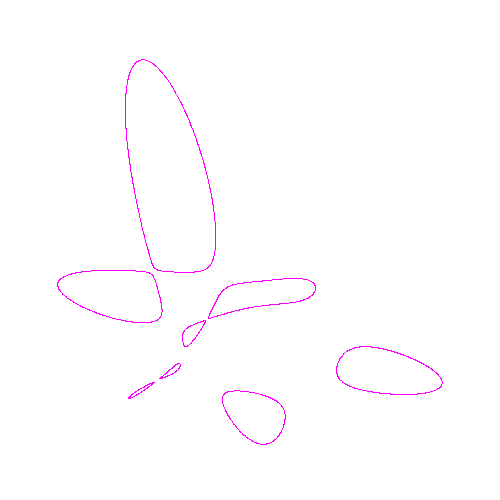
|
|
|
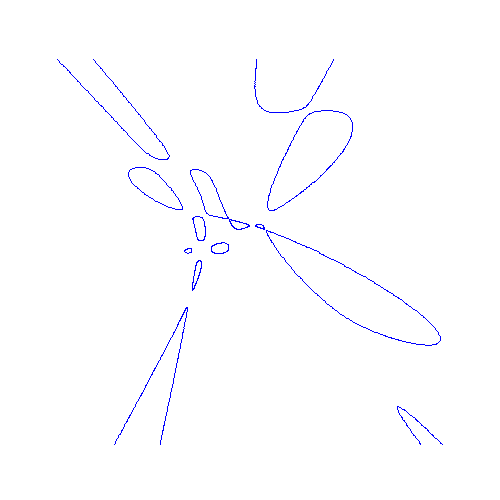
Hessian of sextic with 10 ovals
and 4 unbounded components
|
|
|
|
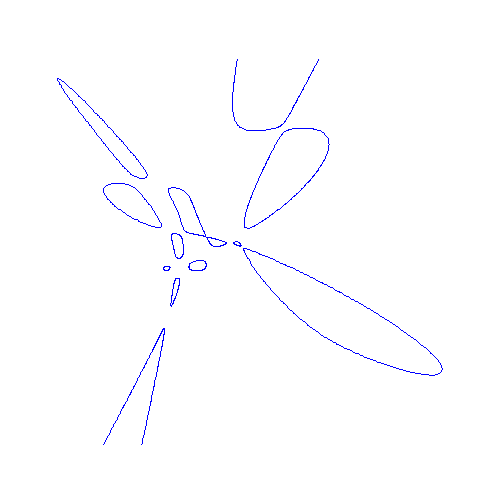
Hessian of sextic with 11 ovals
and 2 unbounded components
|
|
|
|
|
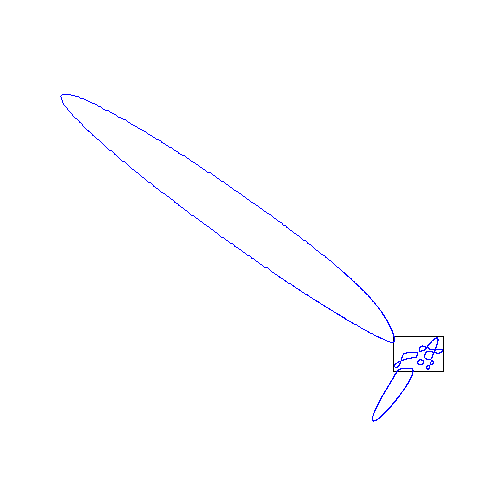
Hessian of sextic with 11 ovals
|
|
|
|
Hessian of sextic with 11 ovals
(close up)
|

|
|
 Hessian of a quartic with 4 compact components
Hessian of a quartic with 4 compact components
 Hessian of a quartic with 2 compact and 4 noncompact components
Hessian of a quartic with 2 compact and 4 noncompact components
 Hessian of a quintic with 6 compact and 4 noncompact components
Hessian of a quintic with 6 compact and 4 noncompact components
 Hessian of a quintic with 7 compact and 2 noncompact components
Hessian of a quintic with 7 compact and 2 noncompact components
 Hessian of a quintic with 8 compact components
Hessian of a quintic with 8 compact components
 Hessian of a sextic with 10 compact and 4 noncompact components
Hessian of a sextic with 10 compact and 4 noncompact components
 Hessian of a sextic with 11 compact and 2 noncompact components
Hessian of a sextic with 11 compact and 2 noncompact components
 Hessian of a sextic with 11 compact components
Hessian of a sextic with 11 compact components