|
README
| |
A copy of this text.
|
|
RealSols.maple
| |
The Maple list of real solutions.
|
|
grab.perl
| |
perl script for parsing the alphaCertified output file
realDistinctSolns.
|
|
sort.maple
| |
Sorts the solutions according to the number of critical points
under the coordinate projections of the 2,2-curve.
|
|
rst.maple
| |
r00.maple,
r22.maple,
r04.maple,
r40.maple,
r44.maple. These draw the (2,2) curve and
crudely draw the workspace of the different mechanisms.
|
|
|
|
| |
These next files draw certain solutions, with the number
17,28,49,104,171 representing the index of the solution
in the list points. The first three are complete, and
were used to create the graphics in our paper, as well as
the animations above.
|
|
171.maple
| |
- The only viable solution. One component of its workspace curve
contains all 9 control points and is a simple closed curve.
|
|
104.maple
| |
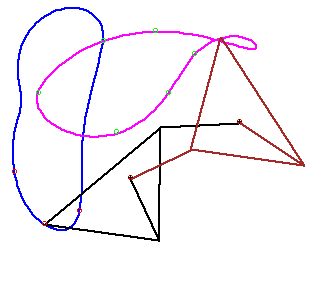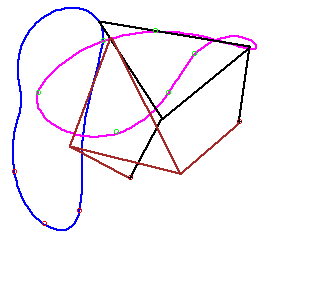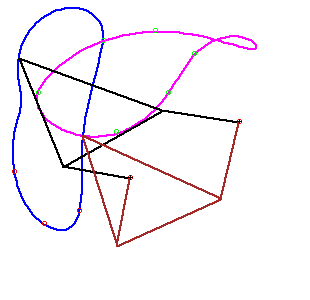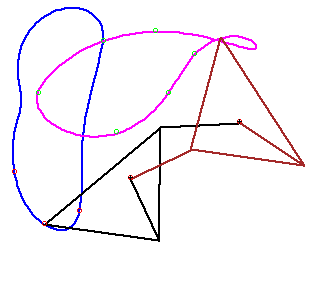
- The workspace is connected, but the curve is not simple closed.
|
|
28.maple
| |
- The workspace is disconnected with the control points lying on
different components.
|
17.maple
49.maple
| |
- These represent early attempts to draw mechanisms, ones which
were not sufficiently interesting to warrant further development
|