Least-Squares Methods for Computational Electromagnetics
 |
 |
 |
Overview
The goal of this project is to develop efficient algorithms for the numerical solution of problems arising from various electromagnetic models. Specifically, we are interested in the system of Maxwell's equations and the related eigenvalue problem. These are important in practical applications, where one needs to compute the electromagnetic field generated by prescribed current and charges, or in the computation of the eigenmodes that will propagate through a given medium.
Our approach is based on a very weak variational formulations of the div-curl systems corresponding to the electrostatic and magnetostatic problems. The finite dimensional approximation is a negative norm finite element least-squares algorithm which uses different solution and test spaces. This allows for approximation of problems with low regularity, where the solution is only in L2 and the data resides in various dual spaces. The solution operators for the above problems are further used to obtain an approximation to the eigenvalue problem.
The resulting discretization method has the advantages of avoiding potentials and the use of Nedelec spaces. In fact, we allow for the mixing of continuous and discontinuous approximation spaces of varying polynomial degrees. Additional advantages are that the matrix of the discrete system is uniformly equivalent to the mass matrix, and that spurious eigenmodes are completely avoided. Finally, the dual inner products can be efficiently implemented using preconditioner for standard second order problems (for example a sweep of multigrid).
Results
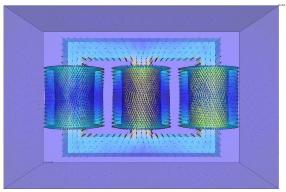
- Magnetic field in a transformer
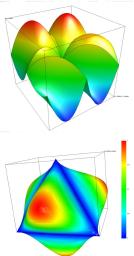
- Eigenmodes of a Fichera corner
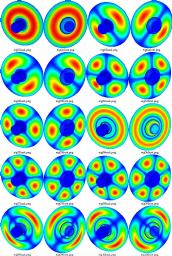
- Eigenmodes of a linear accelerator induction cell
The above results are obtained using a computer program that was developed for the Maxwell equations and the eigenvalue problem in the frequency domain. It is written in C++, in the framework of the AggieFEM finite element library which supports complex geometries, local refinement, multigrid preconditioning and OpenGL visualization. The code is based on the solvers for the magnetostatic and electrostatic problems. It works on triangular, tetrahedral and hexahedral meshes. It provides an eigenvalue solver, which allows for computations of blocks of eigenvalues, and a solver for the full time-harmonic system. A parallel version of this code was implemented based on MPI and CASC's hypre preconditioning library. It uses matrices build in parcsr parallel format, Lobpcg as a parallel eigensolver and BoomerAMG, or ParaSails as a preconditioner.
In these examples we used piecewise constant for each component of the solution space and piecewise linears+face bubbles for each component of the test spaces.
Papers
- A new approximation technique for div-curl systems, by J.H. Bramble and J.E. Pasciak.
- Poster presented at LLNL's 2003 student poster session, by T.V. Kolev and J.E. Pasciak.
