| Exercises |
Orthogonal trajectories
In the spring of 1998, a student solving a problem about orthogonal trajectories wrote the following sentence.
Since the two equations are negative inverses of each other, then the slopes are perpendicular.
If you were this student's instructor in a class on differential equations, what advice would you give the student? (You may assume that the student is a native speaker of English who has above average mathematical ability.)
Modify me
Criticize and rewrite the following sentences.
There are many times in science and mathematics when a list
of data is found by a researcher which, when plotted, looks
almost like a line.
[From a student essay about the method of least
squares approximation, fall 1996.]
First described in the 1940s, scientists were amazed at how
the juvenile cottonmouth uses its tail.
[From a display case at Easterwood Airport,
College Station, May 1999.]
Sign of our times
Comment on this sign seen at the entrance to a campus building in the fall of 1997:
Daylight Saving Time
Find and correct the errors in the following sentence, which appeared on the front page of the Bryan / College Station Eagle on Saturday, October 25, 1997.
Truth in advertising
On December 30, 1997, Karen J.
Cravens posted a report to the
newsgroup rec.humor.funny of receiving a promotional
diskette from an online service advertising "immediate
response-less waiting." Why is this funny?
Hint: there is
a difference between a hyphen and a dash.
In December 2000, an advertisement for telephone services stated, "Service not available in all areas." Why is this funny?
Normal families
Find in the library two books on the subject of normal families: one book about mathematics and the other book about psychotherapy. Photocopy the first page of the first chapter of each book. Which page is easier for an outsider to the field to understand, and why?
Are symbols better than words?
For each of the following six properties, describe in words the class of real-valued functions f on the real line satisfying the property. (For example, your description might use words like "continuous", "bounded", and "constant".)
Kids: don't try this at home
Here are two examples of egregious violations of principles of good mathematical exposition. These examples were created by a professional stunt man, so you should not try to emulate them.
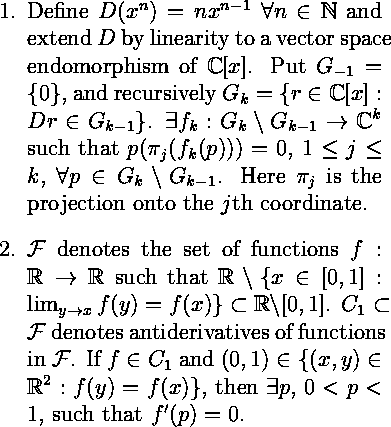
List all the things you can think of that are wrong with these two paragraphs.
Rewrite the examples intelligently and with good style.
 The Math 696 course
pages were last modified April 5, 2005.
The Math 696 course
pages were last modified April 5, 2005.| Exercises |