An Application of Newton's Law of Cooling

Determination of time of death

Police arrive at the scene of a murder at 12 am. They immediately take and record the body's temperature, which is 90^o, and thoroughly inspect the area. By the time they finish the inspection, it is 1:30 am. They again take the temperature of the body, which has dropped to 87^o, and have it sent to the morgue. The temperature at the crime scene has remained steady at 82^o. When was the person murdered?

Solution

Let T(t) be the temperature of the body at time t; take t=0 to be 12 midnight. We have this information.

Time  Body Temp. Ambient Temp.
0 hr     90           82
1.5 hr   87           82

Here, Newton's law of cooling is:

dT/dt=k*(82-T), where k is an unknown constant.

This is a separable ODE. Solve it in these steps.

1. Put it in differential form. (T-82)^-1dT = - k*dt
2. Integrate both sides. ln|T-82|= - k*t + C (Implicit form of solution.)

Next, we need to find k and C in step 2. From the table, we get

ln|90 - 82| = - k*0 + C ( T(0)=90 )

ln|87 - 82| = - 1.5*k + C ( T(1.5)=87 )

Simplifying and solving these, we get C=ln(8) and k=ln(8/5)/1.5. Inserting these in the implicit form of the solution in step 2, and using T(t_D)=98.6 at the time of death, we have

ln|98.6 - 82| = - t_D*ln(8/5)/1.5 + ln(8)

so

t_D = - 1.5*ln(16.6/8)/ln(8/5) = - 2.3296, about 9:40 pm.

t=-3:0.01:3; T=82+8*exp(-0.3133*t);
plot(t,T)
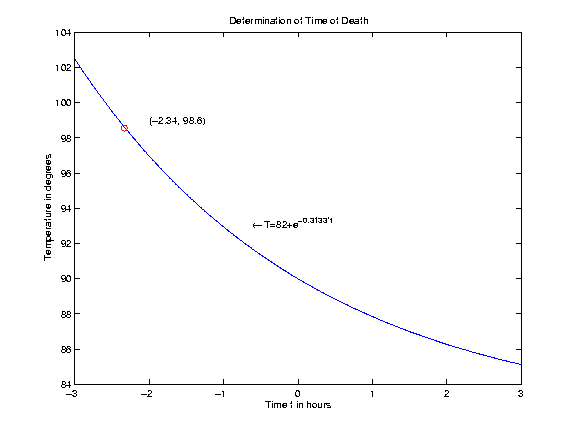
[t_D,T_D]=ginput(1) %Graphically locate the time t_D at which T=98.6

%MATLAB output from the previous command.
t_D =

   -2.3364


T_D =

   98.5614

hold on; plot(t_D,T_D,'or') %Plot the point (t_D,T_D)
title('Determination of Time of Death')
xlabel('Time t in hours'); ylabel('Temperature in degrees')
gtext('\leftarrow T=82+e^{-0.3133*t}') %Put text on graph.
gtext('(-2.3364, 98.5614)') %Put text on graph.
hold off