In section 1.2.3 of the book, we discussed Fourier series for odd function or an even function an interval $[-a,a]$. Recall that when $f$ is odd on $[-a,a]$, we have $\int_{-a}^a f(x)dx =0$, and that when $f(x)$ is even, $\int_{-a}^a f(x)dx =2\int_0^a f(x)dx$. These integrals lead to the following expansions.
because the products $f(x)\cos(n\pi x/a)$ and $f(x)\sin(n \i x/a)$ are respectively even and odd. Thus, f(x) has a Fourier series with only cosine terms, \[ f(x) = a_0+ \sum_{n=1}^\infty a_n\cos(n\pi x/a) \]
because the products $f(x)cos(n \p x/a)$ and $f(x)sin(n\pi x/a)$ are respectively odd and even. Thus, $f(x)$ has a Fourier series with only sine terms, \[ f(x) = \sum_{n=1}^\infty b_n \sin(n\pi x/a) \]
Half-interval expansions Now there is really nothing new in these expansions. We have always made use of symmetry whenever it was possible to do so. Other than simplifying finding series coefficients, why are they important? To answer this question, let's concentrate on the sine series, \[ f(x) = \sum_{n=1}^\infty b_n\sin(n\pi x/a),\ b_n=\frac{2}{a}\int_0^a f(x)\sin(n\pi x/a)dx \]
Observe that bn only depends on values of f(x) on the half interval $[0,a]$, rather than on $[-a,a]$. The point is that if we are given $f(x)$ on $[0,a]$ we can construct an expansion involving only sines. This is important for the heat problem discussed in section 1.1.3.
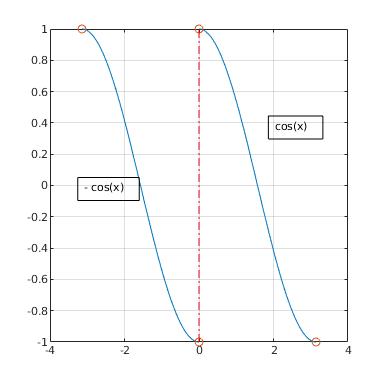
Let's look at an example, with $a=\pi$. This is in fact problem 9 from chapter 1. Suppose that we are given $f(x)=\cos(x)$ on $[0,\pi]$ and that we want a sine series for $f$. The function $f$ is not defined outside of $[0,\pi]$. However, we are free to define it on $[-\pi,0)$. Since we want a sine series, we will make an odd extension to $[-\pi,0)$, $f_{odd}(x)=-\cos(x)$. On $[0,\pi]$ we have $f_{odd}(x)=f(x)=\cos(x)$, because $f_{odd}$ is the same as $f$ on $[0,\pi]$. Here's what it looks like:

The sine series coefficients are
\[ b_n=\frac{2}{\pi} \int_0^\pi \cos(x)\sin(nx)dx=\frac{2}{\pi} \int_0^\pi\big(\frac{1}{2}(\sin((n+1)x) + \sin((n-1)x)\big)dx. \] From this we see that $b_1=0$ and for all $n\ge 2$, \[ b_n =\frac{2}{\pi}\int_{0}^\pi \cos(x)\sin(nx)dx = \frac{-1}{\pi}\bigg( \frac{(-1)^{n+1} -1}{n+1} + \frac{(-1)^{n-1} -1}{n-1}\bigg) =\frac{2n(1+(-1)^{n})}{\pi(n^2-1)}=\begin{cases} \frac{8k}{(4k^2-1)\pi}, & n\ \text(even),\\ 0, & \text{n odd}.\end{cases} \]
Thus the sine series for $cos(x)$ on the half interval $[0,\pi]$ is then \[ \cos(x)=\sum_{k=1}^\infty \frac{8k}{(4k^2-1)\pi}\sin(2kx). \] Note that this series is valid only on $[0,\pi]$, where the $f(x)=\cos(x)$ was defined. Don't be confused by cosine being even on $[-\pi,\pi]$. The sine series comes from the odd extension, $f_{odd}$, as defined above.