The Fourier series f(x) itself is then the sum:
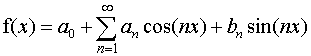wheteher this really gives a number (converges) or not is a question
we'll look at later.
We will be discussing Fourier series for the next few weeks, so we ought to at least have a look at what they are and how they arose.
Sequences & Series For many of you, it's been a while since you thought about sequences and series. So we will begin by giving a brief review of them. By the way, common English usage doesn't distinguish between them. We may speak either of a sequence or a series of events. Mathematical usage does distinguish between them. A sequence of objects - the objects really can be anything at all - is an ordered "list" with entries selected from the objects. For example, we can have a sequence of odd integers, {1,3,5,7, ...}. We can also have a sequence of functions, for example powers of x, {1,x,x2, x3, ...}. Order matters, so the sequences are different if the order is changed. For example, the sequence {3,1,7,5,11,9, ...} is a different sequence than {1,3,5,7, ...}, even though it contains the same objects. Sequences can also be bi-infinite. All odd integers listed in increasing order form a bi-infinite sequence, {...,-5,-3,-1,1,3,5 ...}. Sequences come up in applications. A digital data stream is really a sequence of numbers. So is a discrete-time signal.
The word list is in quotation marks because it doesn't quite capture things precisely. The definition is actually this. A sequence is any function whose domain is a subset of the integers. Very often we will write cn for the value of the function (sequence) c at n, even as we would write f(x) for the value of a function f at x. The notation c[n] is also used. When we do this, we say that cn is the nth term in the sequence. Familiar calculus examples are cn = 1/n or cn=1/n2.
A series is essentially the sum of a sequence. This means that the objects in the range of a sequence (it's a function, so it has a range, remember!) have to be capable of being added to form a series. For the most part, the objects in the range of the sequences we will consider will be numbers (real or complex) or functions themselves. So we can add them - and also multiply them by scalars. In particular, for Fourier series we will deal with sequences of trigonometric functions,
ancos(nx)+bnsin(nx)
The Fourier series f(x) itself is then the sum:
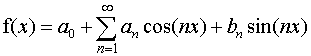wheteher this really gives a number (converges) or not is a question
we'll look at later.
Periodic Functions A function f(x) is periodic with period P if f(x+P) = f(x) for all real values of x. Every multiple of P, 2P, 3P, etc, is also a period. Sums and multiples of functions with period P also have period P. Both sin(x) and cos(x) are periodic with period 2π. The period for ancos(nx)+bnsin(nx) is 2π/n. Of course, these are also 2π periodic, because 2π=n(2π/n). Thus the Fourier series or any part of it is 2π periodic. If f(x) has period P, then we can scale the independent variable x to make the period 2π. To do this, just let t=2πx/P and require g(t)=f(Pt/(2π)). This is useful because we can then work with 2π periodic functions and just rescale the independent variable to get corresponding results for P periodic functions.
Here are a few more odds and ends concerning trigonometric functions. A linear combination of the form
y = a cos(ωt) + b sin(ωt),
where t is time, has period T = 2π/ω. (When time t is the variable, then the period is denoted by T). There are two frequencies associated with it. The angular frequency ω, which is measured in radians per unit time, and the natural frequency, ν, which is measured in cycles per unit time. These are related by ω = 2πν.
Heat Flow and Fourier Series Fourier was an early 19th
century mathematical physicist who was interested in deriving the
physical laws for describing heat flow and in solving problems related
to heat flow. One such problem, finding the temperature in an
insulated bar with ends fixed at 0° and with initial temperature
u(x,0) = f(x), is solved in the text using the method of separation of
variables. We went over the solution to this problem in class. The
result was that, if we ignore the inital conditions, the general
solution has this form:
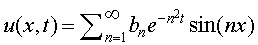To solve the rest of the problem, we must set t = 0 in the equation
and use u(x,0) = f(x) to obtain the coefficients. This is essentially
how Fourier arrived at the idea of representing a function via the
series that bear his name. In the next lecture, we will see how to do
this.