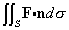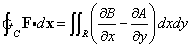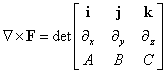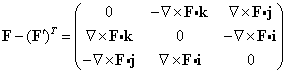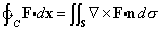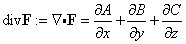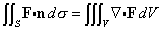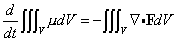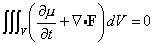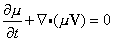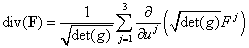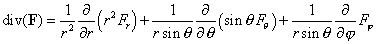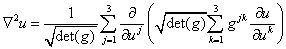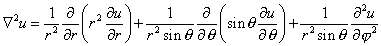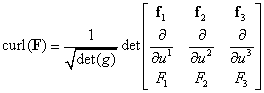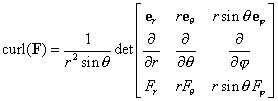- Metric tensors and Jacobian determinants Suppose that
we have written the arclength (ds)2 in u-coordinates, so
that
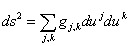
In matrix notation, we can write this as (ds)2 = duTgu du. If we now go from u-coordinates to w-coordinates, du = Jdw, where J = u´ is the Jacobian of the transformation u = u(w). since the arclength is an invariant, we have(ds)2 = dwTJTgu J dw = dwTgw dw.
Consequently, we have that gw = JTgu J. This also can be derived via the covariance of the metric tensor. The matrices involved are all square and n×n. Taking the determinants for both sides, and then taking square roots yieldsdet(gw)1/2 = |det(J)| det(gu )1/2, J = u´(w)
The quantity det(J) is called the Jacobian determinant, and is often writtem as
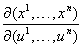 .
.
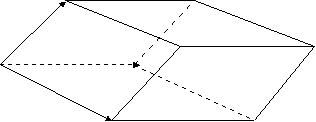
- Jacobi's Theorem Consider a change of coordinates x = x(u), where Rx and Ru correspond to each other under it. Then,
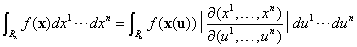
- Invariant volume We want to look at the volume element det(gu )1/2du1...dun when we make the change of coordinates u = u(w). First, we have
det(gu )1/2 du1...dun = det(gu )1/2 |det(u´(w))| dw1...dwn.
Recall that we also have det(gw)1/2 = |det(J)| det(gu )1/2, J = u´(w). Substituting this into the last equation then gives us
det(gu )1/2 du1...dun = det(gw )1/2 dw1...dwn,
which shows that the combination det(gu )1/2 du1...dun is invariant under coordinate transformations. This is often called the invariant volume element.
- Jacobi's Theorem Consider a change of coordinates x = x(u), where Rx and Ru correspond to each other under it. Then,