Math 603-601 - Fall 2002

Assignment 10

1. Compute the line integral
   
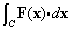
   for the following vector fields and curves.
   
   1. F(x) = (3x-4y)i + (y²+2x)j, where C is the straight line from (0,1) to (1,1) followed by the straight line from (1,1) to (1,2).
   2. F(x) = (3x-y)i + (x+y)j, where C is the circle x²+y² = 4 traversed once in the positive (counterclockwise) direction.
   3. F(x) = (3x²+2y)i + (y-3x)j, where C is the straight line from (1,1) to (2,3).
   4. F(x) = (3x+y-z)i + (zx-xy²)j + 3xyz k, where C is the curve parametrized by x=t, y=t², z=-t, for t=0 to t=2.

2. Find the formula for the gradient in spherical coordinates.

3. Calculate the standard normal for the surface S parametrized by x = u i + v j + f(u,v)k, where R_uv is the rectangle a ≤ u ≤ b, c ≤ v ≤ d. Find an expression for area of S.

4. Consider a surface parametrized by x = x(u¹, u²). Let f₁ = ∂x/∂u¹, f₂ = ∂x/∂u¹. Show that, when x is restricted to the surface, the arc length ds² = dx· dx, satisfies
   ds² = ∑_jk g_jk du^jdu^k
   where g_jk= f_j·f_k are the components of the metric tensor g for the surface. In addition, show that det(g)^1/2 = |N|, where N is the standard normal.

5. Compute the flux integral
   
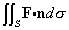
   for the following vector fields and surfaces.
   
   1. F(x) = 3z i + 2x j + y k, where the surface S is the upper half of the hemisphere x²+y²+ z² = 9; the normal direction is upward.
   2. F(x) = zx i - 2xyz j + z² k, where the surface is the curved part of the cylinder x²+y² = 25, with 0 ≤ z ≤ 2. Take the normal as pointing away from the z-axis.

6. Verify Stokes' Theorem

   

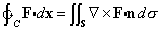
   for F(x) = 2y i - 3z j + x k, with S being the part of the sphere x²+y²+ z² = 4 in the first octant. The normal to S points away from the origin, and C is the positively oriented curve that serves as the boundary of S.

7. Verify the Divergence Theorem

   

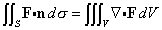
   for F(x) = 2y i + 3x j - z³ k, with S being the surface of the closed cylinder (top, bottom, and curved side) described in Problem 5(b) above.