Math 603-601 - Fall 2002

Assignment 3

1. Consider the column vectors below. Show that these form a basis B for R³. Find a dual basis B^* of row vectors.
   
   

2. Recall that we may parametrize a straight line through the origin via x(t) =tv, where x(t) is the position vector at a "time" t in 2D or 3D.
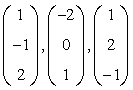
   1. Let z be any point not on the line x(t). Show that q(t) = |x(t) - z|², the square of the distance between x(t) and z, is a quadratic polynomial in t.
   2. Find the value t=t₀ that minimizes q(t), and also q(t₀).
   3. Deduce Schwarz's inequality from the expression for q(t₀).
   4. Show that x(t₀) - z is orthogonal to v.

3. Given that < f,g > = _-1S ¹ f(x)g(x)dx defines an inner product on C[-1,1], find the following:
   1. The norm of f(x)= e^-x.
   2. The norm of g(x)=x.
   3. The angle between f and g.

4. Suppose that <u,v> defines on inner product on a vector space V. Fix a number a>0. Define
   <u,v>_a = a<u,v>
   Show that <u,v>_a defines another inner product on V.

5. Let x and y be vectors in R² and let < x,y > = x₁ y₁ + x₁ y₂ + x₂ y₁ + 2x₂ y₂
   
   1. Show that < x,y > defines an inner product on R².
   2. Using this inner product, calculate the angle bewteen the vectors [1 0]^T and [0 1]^T.
   3. Using this inner product, find all vectors orthogonal to [2 1]^T.