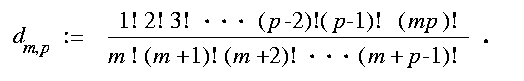



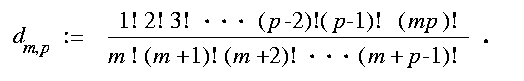 |
Another famous geometric problem is that of conics tangent to five general conics. In 1864 Chasles showed there are 3264 plane conics tangent to five given plane conics.
In 1984 Fulton [Fu] asked if it were possible to choose the 5 conics so that all 3264 tangent conics were real. More generally, he asked if it were possible to do this for other enumerative geometric problems like the questions of Schubert. For us, this asks if one may choose the mp m-planes so that each of the dm,p p-planes are real. This is the case of the problem of 2 lines in P3 meeting 4 given lines, which is not hard to see (a description of the geometry of this case). The first question was answered affirmatively by Fulton (unpublished) and by Ronga, Tognoli, and Vust [RTV]. The second was answered affirmatively when either m or p are 2 by Sottile in his Ph.D. thesis [So94], published as [So97a]. A few other cases of this phenomenon, including the d3,3(=42) 3-planes in C6 meeting 9 general 3-planes nontrivially were settled in [So97b, So97c]. Other examples of this phenomenum include the 40 positions of Stewart platform in robotics [D] and the 12 rational cubics meeting 8 points in P2 [Kh]. (A description of this problem of cubics.)
After the paper on Shapiro's conjecture [So98] was written, Sottile proved this is the case for any enumerative problem involving linear subspaces satisfying special Schubert conditions [So99]. (A special Schubert condition is the condition that a p-plane meets another linear subspace with excess intersection.) It also holds for some problems of enumerating rational normal curves in a Grassmann variety [So00a], and for a large class of enumerative problems involving flag manifolds [So00b]. Even more recently, A. Gabrielov and A. Eremenko gave a proof of the conjecture of Shapiro and Shapiro for Grassmannians of 2-dimensioinal subspaces of a vector space [EG].


