Article for Autumn 2004 issue of
the Emissary, the newsletter of MSRI.
ArXiv.org/math/0501146.
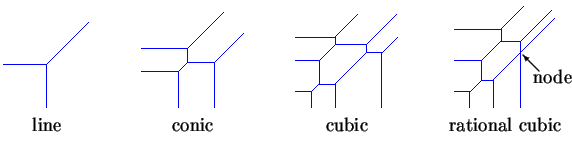
Everyone knows that two points determine a line, and many people who have studied geometry know that five points on the plane determine a conic. In general, if you have m random points in the plane and you want to pass a rational curve of degree d through all of them, there may be no solution to this interpolation problem (if m is too big), or an infinite number of solutions (if m is too small), or a finite number of solutions (if m is just right). It turns out that ``m just right'' means m=3d-1 (m=2 for lines and m=5 for conics).
A harder question is, if m=3d-1, how many rational curves of degree d interpolate the points? Let's call this number Nd, so that N1=1 and N2=1 because the line and conic of the previous paragraph are unique. It has long been known that N3=12, and in 1873 Zeuthen [Ze] showed that N4=620. That was where matters stood until about ten years ago, when Kontsevich and Manin [KM] used associativity in quantum cohomology to give an elegant recursion for this number.
The research themes in the MSRI Winter 2004 semester on Topological Aspects of Real Algebraic Geometry included enumerative real algebraic geometry, tropical geometry, real plane curves, and applications of real algebraic geometry. All are woven together in the unfolding story of this interpolation problem, a prototypical problem of enumerative geometry, which is the art of counting geometric figures determined by given incidence conditions. Here is another problem: how many lines in space meet four given lines? To answer this, note that three lines lie on a unique doubly-ruled hyperboloid.
Enumerative geometry works best over the complex numbers, as the number of real figures depends rather subtly on the configuration of the figures giving the incidence conditions. For example, the fourth line may meet the hyperboloid in two real points, or in two complex conjugate points, and so there are either two or no real lines meeting all four. Based on many examples, we have come to expect that any enumerative problem may have all of its solutions be real [So].
Another such problem is the 12 rational curves interpolating 8 points in the plane. Most mathematicians are familiar with the nodal (rational) cubic shown on the left below. There is another type of real rational cubic, shown on the right.
)
-
N(
)
= 8 .
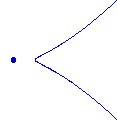
Since there are at most 12 such curves,
N()
+N() \leq 12,
and so there are 8, 10, or 12 real rational cubics interpolating 8
real points in the plane, depending upon the number
(0, 1, or 2) of cubics with an isolated point.
Thus there will be 12 real rational cubics interpolating any 8 of
the 9 points of intersection of the two cubics below.
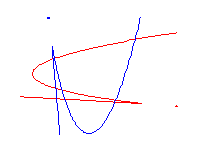
Welschinger [W], who was an MSRI postdoc last Winter, developed this example into a theory. In general, the singularities of a real rational plane curve C are nodes or isolated points. The parity of the number of nodes is its sign s(C), which is either 1 or -1. Given 3d-1 real points in the plane, Welschinger considered the absolute value of the quantity
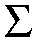s(C) ,
This was a breakthrough, as Wd was
(almost) the first truly non-trivial invariant in enumerative real
algebraic geometry.
Note that Wd is a lower bound for the number of
real rational curves through 3d-1 real points in the plane,
and Wd\leq Nd.
Mikhalkin, who was an organizer of the semester, provided the key to computing Wd using tropical algebraic geometry [Mi]. This is the geometry of the tropical semiring, where the operations of max and + on real numbers replace the usual operations of + and multiplication. A tropical polynomial is a piecewise linear function of the form
Mikhalkin showed that there are only finitely many rational tropical curves of degree d interpolating 3d-1 generic points. While the number of such curves does depend upon the choice of points, Mikhalkin attached positive multiplicities to each tropical curve so that the weighted sum does not, and is in fact equal to Nd. He also reduced these multiplicities and the enumeration of tropical curves to the combinatorics of lattice paths within a triangle of side length d.
Mikhalkin used a correspondence involving the map Log :(C*)2 --> R2 defined by (x,y)|-->(log|x|,log|y|), and a certain `large complex limit' of the complex structure on (C*)2. Under this large complex limit, rational curves of degree d interpolating 3d-1 points in (C*)2 deform to `complex tropical curves', whose images under Log are ordinary tropical curves interpolating the images of the points. The multiplicity of a tropical curve T is the number of complex tropical curves which project to T.
What about real curves? Following this correspondence, Mikhalkin attached a real multiplicity to each tropical curve and showed that if the tropical curves interpolating a given 3d-1 points have total real multiplicity N, then there are 3d-1 real points which are interpolated by N real rational curves of degree d. This real multiplicity is again expressed in terms of lattice paths.
What about Welschinger's invariant? In the same way, Mikhalkin attached a signed weight to each tropical curve (a tropical version of Welschinger's sign) and showed that the corresponding weighted sum equals Welschinger's invariant. As before, this tropical signed weight may be expressed in terms of lattice paths.
During the semester at MSRI, Itenberg, Kharlamov, and Shustin [IKS] used Mikhalkin's results to estimate Welschinger's invariant. They showed that Wd\geq d!/3, and also
There are two other instances of this phenomenon of lower bounds, the first of which predates Welschinger's work. Suppose that d is even and let W(s) be a real polynomial of degree k(d-k+1). Then Eremenko and Gabrielov [EG] showed that there exist real polynomials f1(s),..., fk(s) of degree d whose Wronski determinant is W(s). In fact, they proved a lower bound on the number of k-tuples of polynomials, up to an equivalence. Similarly, while at MSRI, Soprunova and I [SS] studied sparse polynomial systems associated to posets, showing that the number of real solutions is bounded below by the sign-imbalance of the poset. Such lower bounds to enumerative problems, which imply the existence of real solutions, are important for applications.
For example, this story was recounted over beer one evening at the MSRI Workshop on Geometric Modeling and Real Algebraic Geometry in April 2004. A participant, Schicho, realized that the result W3=8 for cubics explained why a method he had developed always seemed to work. This was an algorithm to compute an approximate parametrization of an arc of a curve, via a real rational cubic interpolating 8 points on the arc. It remained to find conditions that guaranteed the existence of a solution which is close to the arc. This was just solved by Fiedler-Le Touzé, an MSRI postdoc who had studied cubics (not necessarily rational) interpolating 8 points to help classify real plane curves of degree 9.