Math 414 - Spring 2004
Lecture 2
Fourier Series - Orthogonality
Relations and Coefficients
In the previous lecture, we discussed
Fourier's solution to the problem of heat flow in a bar of length
π, with a temperature of 0° at each end and an initial
temperature u(x,0)=f(x). The solution to this problem is the
temperature u(x,t) at any time t and any point x along the bar:
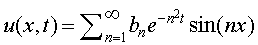 The idea is match the inital conditions to the series above with t=0,
The idea is match the inital conditions to the series above with t=0,
u(x,0)=f(x)=∑n bn sin(nx).
The result is a series for f(x) involving only sines. Had we solved a
similar heat flow problem for a ring of radius 1 instead of a bar,
matching the initial condition u(x,0)=f(x) (x is the angle in radians)
to the corresponding series yield a full Fourier series for f(x), a
series having both sines and cosines:
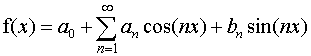 In either case, we are left with the problem of determining the
coefficients from the function.
In either case, we are left with the problem of determining the
coefficients from the function.
Fourier's first approach was messy. He expanded both sides in Taylor
series about x=0, collected terms, and then solved an infinte set of
equations. In the end, he obtained the following expressions for the
coefficients:
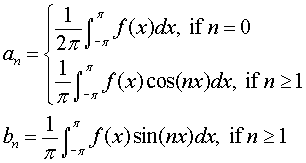 It occurred to Fourier that he might give a simpler proof for these
formulas and derive them under more general conditions if he did two
things. First assume that f(x) has such an expansion and second plug
the series into the expressions he derived by the messy power series
method. With luck, the coefficients should easily appear with much
less work. That is exactly what happens.
It occurred to Fourier that he might give a simpler proof for these
formulas and derive them under more general conditions if he did two
things. First assume that f(x) has such an expansion and second plug
the series into the expressions he derived by the messy power series
method. With luck, the coefficients should easily appear with much
less work. That is exactly what happens.
Before we start our derivation, we will need to have availble a set of
integrals that are called orthogonality relations for the
trigonometric functions. These are in the text, but we'll list them
here, too.
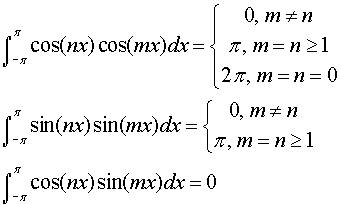
In the chain of equations below, we use what we expect to be the
formula for bn. In the first line we place f(x) by the
corresponding series. We then interchange the sum and the
integral. All of the integrals in the series on the second line can be
evaluated using the orthogonality relations above. In the last, only
πbn remains. Dividing by π then gives the expression
for bn given earlier. A similar derivation applies for the
an.
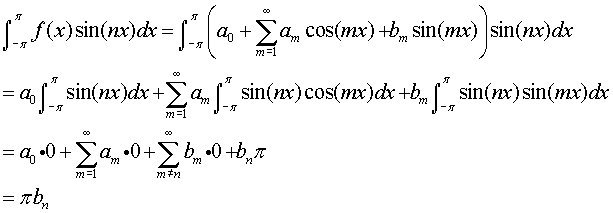 The point is that this is a fairly simple derivation and holds true
under mild assumptions. It also applies in many more situations than
Fourier's original power series method would have.
The point is that this is a fairly simple derivation and holds true
under mild assumptions. It also applies in many more situations than
Fourier's original power series method would have.
We will close this lecture with an example of finding a Fourier
series. Let f(x)=x on the interval [-π,π]. The function itself
has a symmtery property; namely, it's odd. The cosines are all
even functions, and since the product of an even and odd
function is odd, x cos(nx) is odd. Now, the integral of an odd
function over a symmetric integral is odd. It follows that
an=0 for all n. To compute bn, we again employ
the symmetries involved. Since sin(nx) is odd and x is odd, x sin(nx)
is odd, too. Thus, we see that
bn=(2/π)∫0πx sin(nx)dx.
We can evaluate this integral via integration by parts. The result is
∫ x sin(nx)dx = - x cos(nx)/n + sin(nx)/n2 .
Evaluating this between x=0 and x=π and inserting this in the
expression for bn gives
bn=(2/π)(-π cos(n π)/n)=2(-1)n+1/n.
We arrive at x~∑n2(-1)n+1sin(nx)/n =
2sin(x)-2sin(2x)/2+2sin(3x)/3 ...
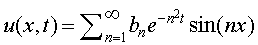 The idea is match the inital conditions to the series above with t=0,
The idea is match the inital conditions to the series above with t=0,
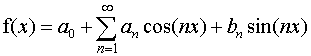 In either case, we are left with the problem of determining the
coefficients from the function.
In either case, we are left with the problem of determining the
coefficients from the function.
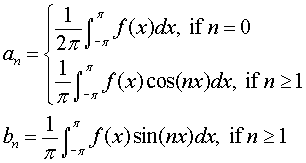 It occurred to Fourier that he might give a simpler proof for these
formulas and derive them under more general conditions if he did two
things. First assume that f(x) has such an expansion and second plug
the series into the expressions he derived by the messy power series
method. With luck, the coefficients should easily appear with much
less work. That is exactly what happens.
It occurred to Fourier that he might give a simpler proof for these
formulas and derive them under more general conditions if he did two
things. First assume that f(x) has such an expansion and second plug
the series into the expressions he derived by the messy power series
method. With luck, the coefficients should easily appear with much
less work. That is exactly what happens.
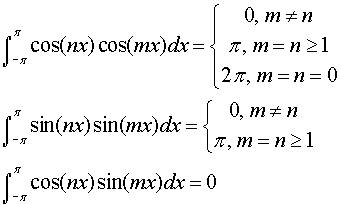
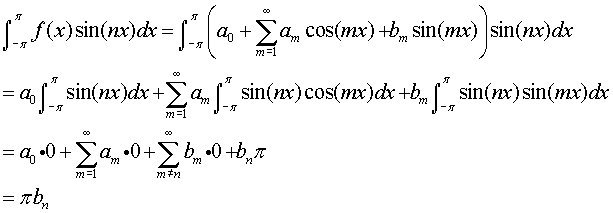 The point is that this is a fairly simple derivation and holds true
under mild assumptions. It also applies in many more situations than
Fourier's original power series method would have.
The point is that this is a fairly simple derivation and holds true
under mild assumptions. It also applies in many more situations than
Fourier's original power series method would have.